Article 4. 변수 변환 2124

Section 2. 분석 변수 처리

• 변수 변환이란 분석을 위해 불필요한 변수를 제거하고, 변수를 반환하며, 새로운 변수를 생성시키는 작업이다.
• 변수들이 선형관계가 아닌 로그, 제곱, 지수 등의 모습을 보일 때 변수 변환을 통해 선형관계로 만들면 분석하기 쉽다.

1. 단순 기능 변환(Simple Functions)

   • 한쪽으로 치우친 변수를 변환하여 분석 모형을 적합하게 하는 방법

     예) 로그 변환(log x), 역수 변환(1/x), 루트 변환(√x), 제곱 변환(x²)

2. 비닝(Binning)

   • 기존 데이터를 범주화하기 위해 사용

   • categorization 기술의 결정은 비즈니스 도메인 지식 필요

   • 두 개 이상 변수의 값에 따라 공변량 비닝(co-variate binning) 수행

     예) 수입을 상, 중, 하의 범주로 나누기

3. 정규화(normalization)

   • 데이터를 특정 구간으로 바꾸는 척도법

   • 최소-최대 정규화, Z-스코어 정규화 유형이 있음

     

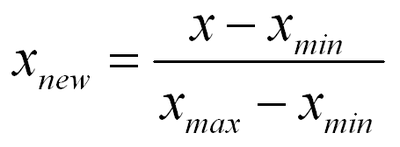
4. 표준화(Standardization)

   • 데이터를 0을 중심으로 양쪽으로 데이터를 분포시키는 방법
   • 표준화와 정규화는 데이터 전처리에서 상호 교환하여 사용

   

Paragraph 1. 단순 기능 변환(Simple Functions Transformation)

변수를 단순한 함수로 변환하는 기능이다.

1. 로그(Logarithm)

   • 변수의 분포를 변경하기 위해서 사용하는 변환 방법

   • 변수들의 분포가 오른쪽으로 기울어진 것을 감소

   • log의 특성상 0과 음수의 값은 적용 불가

     예) 로그 변환(log x)

2. 제곱/세제곱 루트 변환(Square/Cube Root)

   • 로그에 비해서 많이 사용되지는 않는 방법

   • 세제곱 루트 변환은 음수값과 0의 값에 적용 가능

   • 제곱 루트 변환은 0을 포함한 양수 값이 가능

     예) 루트 변환(√x), 세제곱 루트 변환(∛x)

Paragraph 2. 비닝(Binning)

• 비닝은 데이터값을 몇 개의 Bin(혹은 Bucket)으로 분할하여 계산하는 방법이다.
• 데이터 평활화에서도 사용되는 기술이며, 기존 데이터를 범주화하기 위해서도 사용한다.

Paragraph 3. 변수 변환 사례

• 변수 변환은 분석 모델을 만들기 전에 최적화 모델을 만들기 위해 적용한다.
• 일반적으로 마케팅에서 자주 사용되는 변수 변환은 다음과 같다.

변수	일반적인 변환
매출, 판매수량, 가격, 가구소득	log(x)
지리적 거리	1/x, 1/(x²), log(x)
효용에 근거한 시장점유율, 선호점유율	eᶻ/(1+eˣ)
우측으로 꼬리가 긴 분포	√x, log(x)
좌측으로 꼬리가 긴 분포	x²