Article 2. 상관관계 분석 2212

Section 1. 데이터 탐색 기초

Paragraph 1. 상관관계 분석(Correlation Analysis)의 개념

• 상관관계 분석이란 두 개 이사의 변수 사이에 존재하는 상호 연관성의 존재 여부와 연관성의 강도를 측정하여 분석하는 방법이다.
• 예를 들면, A 기업에서 광고비 지출이 매출액의 증가에 어느 정도의 영향이 있는지를 파악할 때 사용하는 방법이다.

Paragraph 2. 변수 사이의 상관관계의 종류

종류	설명
양(+)의 상관관계	• 한 변수의 값이 증가할 때 다른 변수의 값도 증가하는 경향을 보이는 상관관계 • 강도에 따라 강한 양의 상관관계, 약한 양의 상관관계가 있음
음(-)의 상관관계	• 한 변수의 값이 증가할 때 다른 변수의 값은 반대로 감소하는 경향을 보이는 상관관계 • 강도에 따라 강한 음의 상관관계, 약한 음의 상관관계가 있음
상관관계 없음	• 한 변수의 값의 변화에 무관하게 다른 변수의 값이 변하는 상관관계

Paragraph 3. 상관관계의 표현 방법

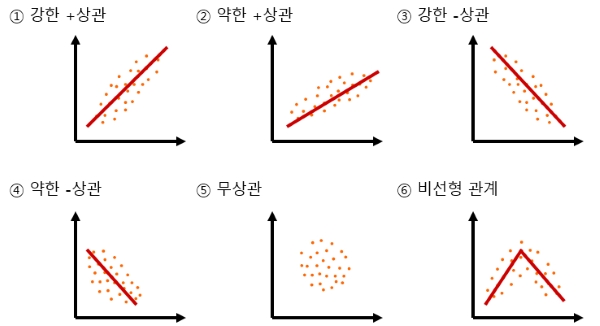
Subparagraph 1. 산점도(Scatter Plot)를 통한 표현 방법

변수 사이의 관계를 산점도 그래프를 통하여 표현하는 방법이다.

Subparagraph 2. 공분산을 통한 표현 방법

Clause 1. 공분산(Covariance)의 개념

공분산은 2개의 변수 사이의 상관 정도를 나타내는 값이다.

Clause 2. 공분산의 수학적 정의

Clause 3. 공분산 해석

공분산 값	내용
( Cov > 0 )	2개의 변수 중 하나의 값이 상승하는 경향을 보일 때, 다른 값도 상승하는 경향을 보인다면 공분산의 값은 양수가 됨
( Cov < 0 )	2개의 변수 중 하나의 값이 상승하는 경향을 보일 때, 다른 값이 하강하는 경향을 보인다면 공분산의 값은 음수가 됨

Clause 4. 공분산 특징

• 상관관계의 상승 혹은 하강하는 경향을 이해할 수 있다.
• 공분산 값의 크기는 측정 단위에 따라 달라지므로 선형관계의 강도를 나타내지는 못한다.

Subparagraph 3. 상관계수(Correlation Coefficient)를 통한 표현 방법

• 두 변수 사이의 연관성을 수치적으로 객관화하여 두 변수 사이의 방향성과 강도를 표현하는 방법이다.
• 상관계수(r)의 범위 : -1 ≤ r ≤ 1 (상관계수가 절댓값 1에 가까울수록 강한 상관관계)

r값	관계
0.7 ≤ r ≤ 1	강한 양의 선형관계
0.3 ≤ r < 0.7	뚜렷한 양의 선형관계
0.1 ≤ r < 0.3	약한 양의 선형관계
-0.1 < r < 0.1	거의 무시될 수 있는 선형관계
-0.3 < r ≤ -0.1	약한 음의 선형관계
-0.7 < r ≤ -0.3	뚜렷한 음의 선형관계
-1 ≤ r ≤ -0.7	강한 음의 선형관계

Paragraph 4. 상관관계 분석의 분류

Subparagraph 1. 변수의 개수에 따른 분류

분석의 대상이 되는 변수의 개수가 두 개일 경우 단순 상관 분석이라고 하고, 변수의 개수가 3개 이상일 경우 다중 상관 분석이라고 한다.

1. 단순 상관 분석

   • 두 개의 변수 사이의 상관성 분석

     나이와 급여 사이의 상관성 분석

2. 다중 상관 분석

   • 세 개 이상의 변수 사이의 상관성 분석

     직위, 나이, 급여 사이의 상관성 분석

Subparagraph 2. 변수의 속성에 따른 분류

분석의 대상이 되는 변수의 속성에 따라 수치적 데이터, 명목적 데이터, 순서적 데이터 등으로 분류할 수 있다.

1. 수치적 데이터

   • 수치형 데이터인 등간 척도, 비율 척도에 해당

   • 수치로 표현을 할 수 있는 측정 가능한 데이터 변수

     예) 나이, 몸무게, 이동 거리

   • 변수의 연상이 가능

     예) 이동거리의 평균

   • 분석 방법

     • 피어슨(Pearson) 상관계수

2. 순서적 데이터

   • 범주형 데이터 중에서 순서적 데이터에 해당

   • 데이터의 순서에 의미를 부여한 데이터 변수

     예) 성적 순위(1등, 2등, 3등), 학력(대졸, 고졸, 중졸)

   • 변수의 연산이 불가능

     예) ‘고졸 + 중졸 = 대졸’로 표현 불가능

   • 분석 방법

     • 스피어만(Spearman) 순위 상관 분석

3. 명목적 데이터

   • 범주형 데이터 중에서 명목척도에 해당

   • 데이터의 특성을 구분하기 위하여 숫자나 기호를 할당한 데이터 변수

     예) 성별(남/여), 학반(1반, 2반, 3반)

   • 변수의 연산이 불가능

     예) ‘1반 + 2반 = 3반’으로 표현 불가능

   • 분석 방법

     • 카이제곱(χ2) 검정(교차 분석)

Clause 1. 수치적 데이터의 상관성 분석

• 두 변수가 키와 몸무게, 수입과 지출 등과 같은 수치적 데이터일 경우에 두 변수 사이의 연관성을 계량적으로 산출하여 분석하는 방법이다.
• 수치적 데이터의 상관 분석에서 피어슨 상관계수 방법을 일반적으로 사용한다.
• 전제조건 : 두 변수의 분산이 동일하다는 전제조건 아래에서 사용한다.

	=	correlation coefficient
	=	values of the x-variable in a sample
	=	mean of the values of the x-variable
	=	values of the y-variable in a sample
	=	mean of the values of the y-variable

Clause 2. 명목적 데이터의 상관성 분석

• 두 변수가 지역(서울, 대구, 부산)과 종고(불교, 기독교, 천주교)와 같은 명목적 데이터일 경우에 두 변수 사이의 연관성은 χ2(Chi-Squared; 카이제곱) 검정을 통하여 분석한다.
• 데이터에 대한 분류의 의미를 지닌 명목적 데이터 변수 사이의 상관계수를 계산 하는 것은 큰 의미가 없다.
• 카이제곱 검정은 교차 분석이라고도 불린다.

Clause 3. 순서적 데이터의 상관성 분석

• 두 변수가 언어 성적 순위(1등, 2등, 3등)와 수리 영역 순위(1등, 2등, 3등) 같은 순서적 데이터일 경우에 두 변수 사이의 연관성을 계량적으로 산출하여 분석하는 방법이다.
• 순서적 데이터의 분석에는 스피어만 순위상관계수를 이용하여 분석한다.