Article 4. 시각적 데이터 탐색 2214
Section 1. 데이터 탐색 기초
데이터 탐색에서 주로 사용되는 시각화 도구는 히스토그램, 막대형 그래프, 박스 플롯, 산점도이다.
Paragraph 1. 히스토그램
Subparagraph 1. 히스토그램(Histogram) 개념
히스토그램은 자료 분포의 형태를 직사각형 형태로 시각화하여 보여주는 그래프이다.
Subparagraph 2. 히스토그램 특징
- 히스토그램의 가로축은 수치형 데이터이다.
- 히스토그램의 막대는 서로 붙어 있다.
- 히스토그램의 막대 넓이는 일정하다.
Paragraph 2. 막대형 그래프
Subparagraph 1. 막대형 그래프(Barplot) 개념
여러 가지 항목들에 대한 많고 적음을 비교하기 쉽도록 수량을 막대의 길이로 표현하는 그래프이다.
Subparagraph 2. 막대형 그래프 특징
- 막대형 그래프의 가로축은 수치형 데이터가 아니어도 된다.
- 막대형 그래프의 막대는 서로 떨어져 있다.
- 막대형 그래프의 막대 넓이는 같지 않을 수 있다.
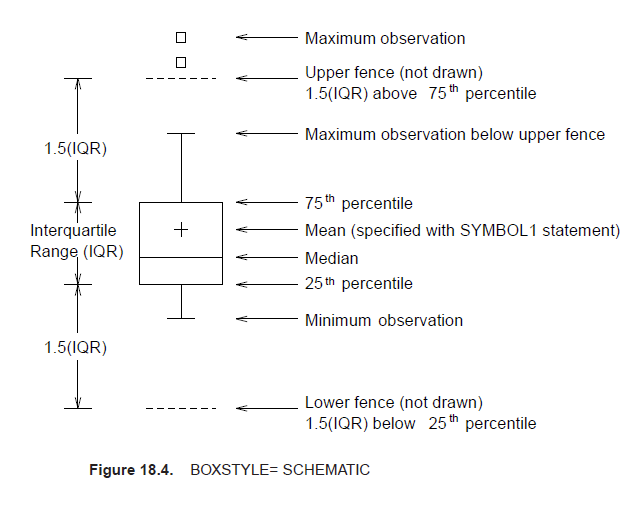
Paragraph 3. 박스 플롯
Subparagraph 1. 박스 플롯(Boxplot)의 개념
- 많은 데이터 그림을 이용하여 집합의 범위와 중앙값을 빠르게 확일할 수 있으며, 또한 통계적으로 이상값이 있는지 빠르게 확인이 가능한 시각화 기법이다.
- 박스 플롯은 상자 수염 그림(Box-and-Whisker Plot), 상자 그림 등 다양한 이름으로 불린다.
Subparagraph 2. 박스 플롯의 구성요소
| 구성요소 | 설명 |
|---|---|
| 하위 경계 | • 제1 사분위에서 1.5 IQR을 뺀 위치 |
| 최솟값 | • 하위 경계 내의 관측치의 최솟값 |
| 제1 사분위(Q_1) | • 자료들의 하위 25%의 위치를 의미 |
| 제2 사분위(Q_2; 중위수) | • 자료들의 50%의 위치로 중앙값(Median)을 의미 • 두꺼운 막대로 가시성을 높여서 표현 |
| 제3 사분위(Q_3) | • 자료들의 하위 75%의 위치를 의미 |
| 최댓값 | • 상위 경계 내의 관측치의 최댓값 |
| 상위 경계 | • 제3 사분위에서 IQR의 1.5배 위치 |
| 수염(Whiskers) | • Q_1, Q_3로부터 IQR의 1.5배 내에 있는 가장 멀리 떨어진 데이터까지 이어진 선 |
| 이상값(Outlier) | • 수염보다 바깥쪽에 데이터가 존재한다면, 이것은 이상값으로 분류 |
Paragraph 4. 산점도(Scatter Plot)
- 가로축과 세로축의 좌표평면상에서 각각의 관찰점들을 표시하는 시각화 방법이다.
- 2개의 연속형 변수 간의 관계를 보기 위하여 사용된다.