Article 1. 데이터 요약 2311

Section 1. 기술 통계

• 기술통계란 데이터 분석의 목적으로 수집된 데이터를 확률·통계적으로 정리·요약하는 기초적인 통계이다.
• 기술통계는 분석의 초기 단계에서 데이터 분포의 특징을 파악하려는 목적으로 주로 산출한다.
• 통계적 수치를 계산하고 도출(평균, 분산, 표준 편차)하거나 그래프를 활용(막대 그래프, 파이 그래프)하여 데이터에 대한 전반적인 이해를 돕는다.

Paragraph 1. 기초 통계량

Subparagraph 1. 평균(Mean)

• 자료를 모두 더한 후 자료 개수로 나눈 값이다.
• 전부 같은 가중치를 두지만, 이상값에 민감한 단점이 있다.
• 평균에는 표본평균, 모평균, 가중평균이 있다.
• 표본(Sample)은 조사하는 모집단의 일부분이다.

1. 표본평균

   • 표본조사를 통해 얻은 n개의 데이터가 X_1, X_2, … , X_n 일 때 표본에 대한 평균

     

2. 모평균

   • 모집단 X_1, X_2, … , X_n 에 대한 평균

   • 표본평균과 구분하기 위해 ‘𝜇’를 사용하며 ‘뮤’라고 읽음

     

Subparagraph 2. 중위수(Median)

• 모든 데이터값을 크기 순서로 오름차순 정렬하였을 때 중앙에 위치한 데이터값으로 중앙값이라고도 한다.
• 특이값에 영향을 받지 않는다.
• 데이터값의 수가 홀수일 경우에는 중위수가 하나가 되지만 데이터값의 수가 짝수일 경우에는 중앙에 위치한 두개의 값을 평균으로 하여 중위수를 구한다.

Subparagraph 3. 최빈수(Mode)

• 데이터값 중에서 빈도수가 가장 높은 데이터값이다.
• 주어진 데이터 중에서 가장 많이 관측되는 수이다.

Subparagraph 4. 범위(Range)

데이터값 중에서 최대 데이터값(Max)과 최소 데이터값(Min) 사이의 차이이다.

Subparagraph 5. 분산(Variance)

데이터가 평균으로부터 흩어진 정도를 나타내는 기초통계량이다.

1. 표본 분산

   • 평균이 x̅인 n개의 데이터값 X_1, X_2, … , X_n 일 때, 각 데이터값과 평균과의 차이인 편차(Deviation)를 구함

   • 양의 편차와 음의 편차를 더할 때 0이 될 수 있으므로 각 데이터값을 제곱 후 모두 더함

   • 더한 값을 (n-1)로 나눔

     

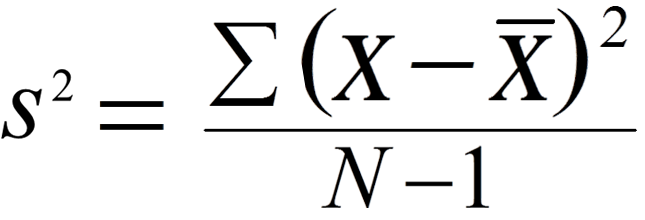
2. 모분산

   • 평균이 𝜇이고 표본의 분산과 동일한 방법으로 모집단의 분산을 계산함

   • 모집단은 N으로 나눔

   • 모집단에 대한 분산은 𝛔²으로 정의

     

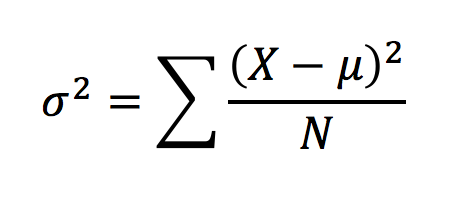
Subparagraph 6. 표준편차(Standard Deviation)

표준편차는 분산에 양의 제곱근을 취한 값이다.

1. 표본의 표준편차
   • 표본의 분산에 양의 제곱근을 취함
2. 모집단의 표준편차
   • 모분산에 양의 제곱근을 취함

Subparagraph 7. 평균의 표준 오차(Standard Error of Mean)

• 표본 평균의 표본 추추 분포에 대한 표준 편차이다.
• 모집단으로부터 수 많은 표본들을 추출한 후 각 표본들에 대한 평균을 구하고, 각 평균들에 대한 전체 평균을 다시 구한 값으로 각 평균들이 전체 평균으로부터 평균적으로 얼마나 떨어져 있는지를 나타낸 값이다.

Subparagraph 8. 분포(Distribution)

데이터 분포의 형태와 대칭성을 설명할 수 있는 통계량에는 첨도와 왜도가 있다.

1. 첨도(Kurtosis)

   • 데이터 분포의 ‘뾰족한 정도’를 설명하는 통계량

   • 첨도의 값이 0이면 집단의 분포가 표준 정규 분포와 뾰족한 정도가 같음을 의미

     

2. 왜도(Skewness)

   • 데이터 분포의 ‘기울어진 정도’를 설명하는 통계량

   • 비대칭성을 나타내는 통계량

     

Paragraph 2. 상관 분석

Subparagraph 1. 상관 분석(Correlation Analysis) 개념

• 상관 분석은 두 개 이상의 변수 간에 존재하는 연관성의 정도(하나의 변수가 다른 변수와 어떤 연관성을 가지고 변화하는가)를 측정하여 분석하는 방법이다.

분석 방법	설명
단순상관 분석	두 변수 사이의 연관 정보를 알아내는 분석
다중상관 분석	셋 또는 그 이상의 변수들 사이의 연관 정도를 분석

• 데이터의 속성에 따라서 수치적, 명목적, 순서적 데이터 등을 가지는 변수 간의 상관 분석이 있다.

Subparagraph 2. 상관 분석의 종류

Clause 1. 수치적 데이터 변수의 상관 분석

• 수치적 데이터 변수로 이루어진 두 변수 간의 선형적 연관성을 계량적으로 파악하기 위한 통계적 기법이다.

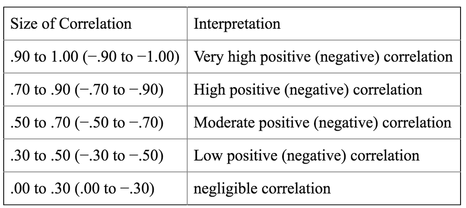
• 일반적으로 피어슨 상관계수를 선형관련성 정도로 측정하는 척도로 사용한다.

  

  ⬇피어슨 상관계수 해석

  ![Everything you need to know about interpreting correlations

  by Zakaria Jaadi

  Towards Data Science](https://miro.medium.com/max/932/1*Qz_gwy4ZaSZuOpl3IyO2HA.png)

Clause 2. 명목적 데이터 변수의 상관 분석

• 항목들을 분류하기 위한 명목적 데이터 변수들로 이루어진 두 변수 간의 연관성을 계량저긍로 파악하기 위한 통계적 기법이다.
• 명목적 변수들로 구성된 분류표상의 발생빈도를 기반으로 명목적 데이터 변수간의 연관성을 추론하기 위한 χ² 검정을 사용한다.
• 수치적 데이터 변수와 달리 분류의 의미를 지닌 명목적 데이터 변수 간의 상관계수를 계산하는 것이 큰 의미가 있지 않다.

Clause 3. 순서적 데이터 변수의 상관 분석

• 순서가 중요한 의미가 있는 순서적 데이터 변수들로 이루어진 두 변수 간의 연관성 및 상관관계를 검정하기 위한 통계적 분석기법이다.
• 순서적 데이터 변수의 상관 분석은 스피어만 순위상관계수를 통해서 분석을 수행한다. (스피어만 순위상관계수는 원 데이터 대신 순위를 이용하여 상관계수를 결정)

Paragraph 3. 회귀 분석

Subparagraph 1. 회귀 분석(Regression Analysis) 개념

• 회귀 분석은 하나 이상의 독립변수들이 종속변수에 미치는 영향을 추정할 수 있는 통계기법이다.
• 회귀 분석 모델은 독립변수와 종속변수의 개수 및 형태에 따라서 다양한 세부 모델들로 분류한다.

Subparagraph 2. 회귀 분석 모형의 종류

1. 단순 회귀 모형
   • 독립변수와 종속변수가 1개씩이면서 모두 수치형 변수인 경우
2. 다중 회귀 모형
   • 2개 이상의 독립변수이면서 수치형 혹은 범주형
   • 1개의 수치형 종속변수

회귀 분석 모형을 도출한 이후에는 이에 대한 적합성을 평가해야 한다.

Subparagraph 3. 회귀 분석 모형의 적합성 평가

• 객관적으로 도출된 회귀식이 통계적으로 유의한지를 평가하기 위해 분산 분석표를 활용한다.
• 모형이 얼마나 잘 설명력을 가지는지를 확인하기 위해서는 결정계수 R²을 확인한다.
• 회귀 분석 결과를 신뢰하고 효과적으로 활용하기 위해 5가지 전제조건이 있다.

전제조건	설명
선형성	독립변수와 종속변수 간에는 선형관계가 존재
등분산성	잔차(추정오차)들은 같은 분산을 가짐
독립성	잔차와 독립변수의 값이 관련돼 있지 않음
비상관성	관측치들의 잔차들끼리 상관이 없어야 함
정규성	잔차는 평균이 0이고 분산이 𝛔²인 정규 분포를 따름

• 이상의 가정들 만족 여부는 잔차들의 그래프를 통해 확인한다.

Subparagraph 4. 독립변수 선택 방법

• 회귀모델에서 종속변수와 독립변수들을 어떻게 선택할지는 중요한 사안이다.
• 독립변수 선택 방법으로는 후진 제거법, 전진 선택법, 단계적 방법이 있다.

선택방법	설명
후진 제거법(Backward Elimination)	• 모든 독립변수를 사용하여 하나의 회귀식을 수립 • 회귀식에서 중요하지 않은 독립변수 값들에 대한 검정을 한 후, 그 값이 가장 작은 변수부터 차례로 제거하고 남은 나머지 독립변수들을 바탕으로 회귀식을 다시 추정하는 방법
전진 선택법(Forward Selection)	• 종속변수에 가장 큰 영향을 줄 것으로 판단되는 하나의 독립변수를 이용하여 회귀식을 수립한 후, 단계마다 중요하다고 판단되는 독립변수를 하나씩 회귀식에 추가하여 회귀모델을 다시 추정하여 새로운 독립변수의 부분 검정을 통해 중요 정도를 계산하는 방법
단계적 방법(Stepwise Method)	• 후진 제거법과 전진 선택법의 절충적인 형태 • 전진 선택법에 따라 종속변수에 가장 큰 상관관계가 있는 독립변수를 택함과 동시에 각 단계에서 후진 제거법과 같이 회귀식에서 중요하지 않은 독립변수를 제거하는 방법

Paragraph 4. 분산 분석

Subparagraph 1. 분산 분석(ANOVA; Analysis of Variance) 개념

두 개 이상의 집단 간 비교를 수행하고자 할 때 집단 내의 분산, 총 평균과 각 집단의 평균 차이에 의해 생긴 집단 간 분산 비교로 얻은 F-분포를 이용하여 가설검정을 수행하는 방법이다.

Subparagraph 2. 분산 분석 특징

• 검정 통계량인 F-검정 통계량 값은 집단 내 분산 대비 집단 간 분산이 몇 배 더 큰지를 나타내는 값으로 해석된다.
• 분산 분석은 복수의 집단을 비교할 때 분산을 계산함으로써 집단 간에 통계적인 차이가 있다고 할 수 있는지, 혹은 차이가 없다고 할 수 있는지를 판정하는 분석 방법이다.

Subparagraph 3. 분산 분석 종류

분산 분석은 독립변수와 종속변수의 수에 따라서 일원분산 분석, 이원분산 분석, 다변량 분산 분석, 공분산 분석으로 나눌 수 있다.

종류	설명
일원분산 분석	• 집단을 나누는 요인인 독립변수가 1개이고 종속변수도 1개인 경우 • 독립변수에 의한 집단 사이의 종속변수 평균 차이를 비교하기 위한 분석
이원분산 분석	• 독립변수가 2개이고 종속변수가 1개일 경우에서 집단 간 종속변수의 평균차이를 분석하는 방법
다변량 분산 분석	• 종속변수가 2개 이상인 경우에 집단 간 종속변수의 평균 차이를 비교하는 방법
공분산 분석	• 연속형 외생변수가 종속변수에 미치는 영향을 제거한 후, 순수한 집단 간 종속변수의 평균 차이를 평가하는 방법

Paragraph 5. 주성분 분석

Subparagraph 1. 주성분 분석(PCA; Principal Component Analysis) 개념

많은 변수의 분산방식(분산⋅공분산)의 패턴을 간결하게 표현하는 주성분 변수를 원래 변수의 선형 결합으로 추출하는 통계기법이다.

Subparagraph 2. 주성분 분석 특징

• 주성분 변수는 원래 변수 정보를 축약한 변수이며, 일부 주성분에 의해 원래 변수의 변동이 충분히 설명되는지 알아보는 분석 방법이다.
• P개의 변수가 있는 경우 이를 통해 얻은 정보를 P보다 상당히 적은 K개의 변수로 요약하는 것이다.
• 가장 적은 수의 주성분을 사용하여 분산의 최대량을 설명한다.

Paragraph 6. 판별 분석

Subparagraph 1. 판별 분석(Discriminant Analysis) 개념

집단에 대한 정보로부터 집단을 구별할 수 있는 판별규칙 혹은 판별함수를 만들고, 다변량 기법으로 조사된 집단에 대한 정보를 활용하여 새로운 개체가 어떤 집단이지를 탐색하는 통계기법이다.