Article 3. 확률분포 2313

2 minute read

Section 1. 기술 통계

Paragraph 1. 확률분포(Probability Distribution) 개념

확률분포란 확률변수가 특정한 값을 가질 확률을 나타내는 분포이다.
확률분포는 확률변슈의 종류에 따라 크게 이산확률분포와 연속확률분포로 나뉜다.

Paragraph 2. 확률분포의 종류

Subparagraph 1. 이산확률 분포

Clause 1. 이산확률분포(Discrete Probability Distribution) 개념

이산확률분포는 이산확률변수 X가 가지는 확률분포이다.
이산확률변수는 확률변수 X가 0, 1, 2, 3, … 와 같이 하나씩 셀 수 있는 값을 취한다.

Clause 2. 이산확률분포 종류

이산확률분포의 종류로는 포아송 분포, 베르누이 분포, 이항분포 등이 있다.

포아송 분포

이산형 확률 분포 중 주어진 시간 또는 영역에서 어떤 사건의 발생 횟수를 나타내는 확률분포

정해진 시간 안에 어떤 사건이 일어날 횟수에 대한 기댓값을 λ라고 했을 때, 그 사건이 X회 일어날 확률 분포

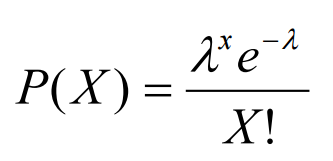![Probability Distributions In Data Science Pier Paolo Ippolito](http://makemeanalyst.com/wp-content/uploads/2017/05/Poisson-Distribution-Formula.png)

기댓값: E(X) = λ
분산: V(X) = λ

베르누이 분포
- 특정 실험의 결과가 성공 또는 실패로 두 가지의 결과 중 하나를 얻는 확률분포
  
  P = p
- 기댓값: E(X) = p
- 분산: V(X) = p(1-p)

이항 분포

n번 시행 중에 각 시행의 확률이 p일 때, k번 성공할 확률분포

$P_{x} = {n \choose x} p^{x} q^{n-x}$

= binomial probability

= number of times for a specific outcome within n trials

${n \choose x}$ = number of combinations

= probability of success on a single trial

= probability of failure on a single trial

= number of trials

n과 k가 1이면 베르누이 시행
기댓값: E(X) = np
분산: V(X) = p(1-p)

	=	binomial probability
	=	number of times for a specific outcome within n trials
${n \choose x}$	=	number of combinations
	=	probability of success on a single trial
	=	probability of failure on a single trial
	=	number of trials

Subparagraph 2. 연속확률분포

Clause 1. 연속확률분포(Continuous Probability Distribution) 개념

확률변수 X가 실수와 같이 연속적인 값을 취할 때는 이를 연속확률변수라 하고 이러한 연속확률변수 X가 가지는 확률분포를 연속확률분포라 한다.

Clause 2. 연속확률분포 종류

연속확률 분포의 종류에는 정규 분포, 표준 정규 분포, T-분포, 카이제곱 분포, F-분포 등이 있다.

정규분포

모평균이 μ, 모분산이 σ²이라고 할 때, 종 모양의 분포

$f(x)= {\frac{1}{\sigma\sqrt{2\pi}}}e^{- {\frac {1}{2}} (\frac {x-\mu}{\sigma})^2}$

= probability density function

$\sigma$ = standard deviation

$\m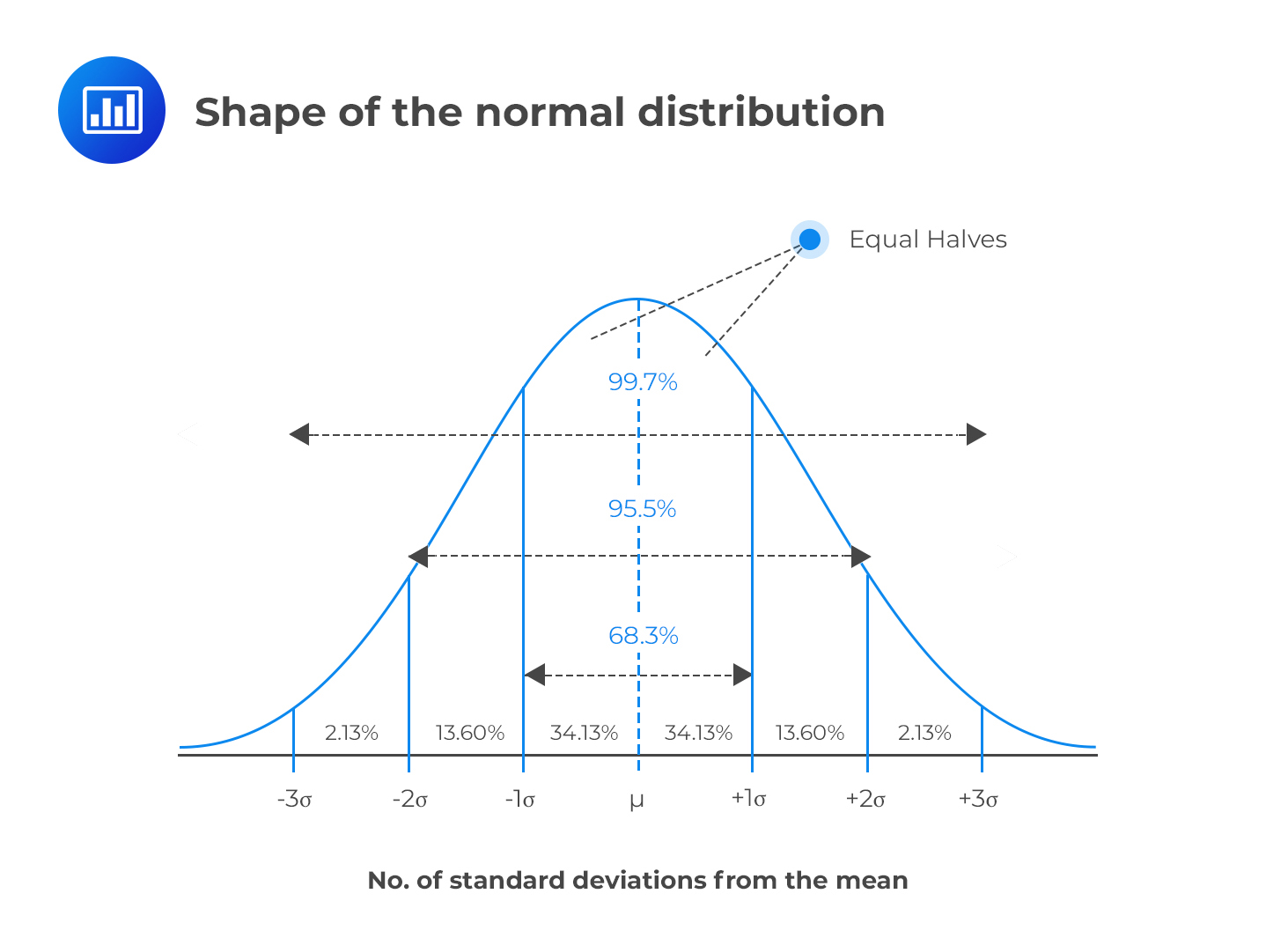u$ = mean

![Key Properties of the Normal distribution CFA Level 1 - AnalystPrep](https://analystprep.com/cfa-level-1-exam/wp-content/uploads/2019/10/page-123.jpg)

![Standard Normal Distribution - an overview ScienceDirect Topics](https://ars.els-cdn.com/content/image/3-s2.0-B9780128051634000049-u04-02-9780128051634.jpg)

기댓값: E(X) = μ
분산: V(X) = σ²

	=	probability density function
$\sigma$	=	standard deviation
$\mu$	=	mean

표준정규분포(Z-분포)

정규 분포 함수에서 X를 Z로 정규화한 분포

$Z = \frac{x - \mu}{\sigma}$

= standard score

= observed value

$\mu$ = mean of the sample

$\sigma$ = standard deviation of the sample

![The Standard Normal Distribution Examples, Explanations, Uses](https://cdn.scribbr.com/wp-content/uploads/2020/10/standard-normal-distribution.png)

기댓값: E(X) = 0
분산: V(X) = 1

	=	standard score
	=	observed value
$\mu$	=	mean of the sample
$\sigma$	=	standard deviation of the sample

T-분포

정규 분포의 평균(μ)의 해석에 많이 쓰이는 분포

모집단이 정규 분포라는 정도만 알고, 모 표준편차(σ)는 모를 때 사용

$t =\frac{\bar{x}-\mu}{s / \sqrt{n}}$

= Student’s t-distribution

$\bar{x}$ = sample mean

$\mu$ = population mean

= sample standard deviation

= sample size

기댓값: E(X) = 0
분산: V(X) = k/(k-2) (단, k는 자유도)

𝛘² 분포(카이제곱-분포)
- K개의 서로 독립적인 표준 정규 확률변수를 각각 제곱한 다음 합해서 얻어지는 분포
- K는 자유도
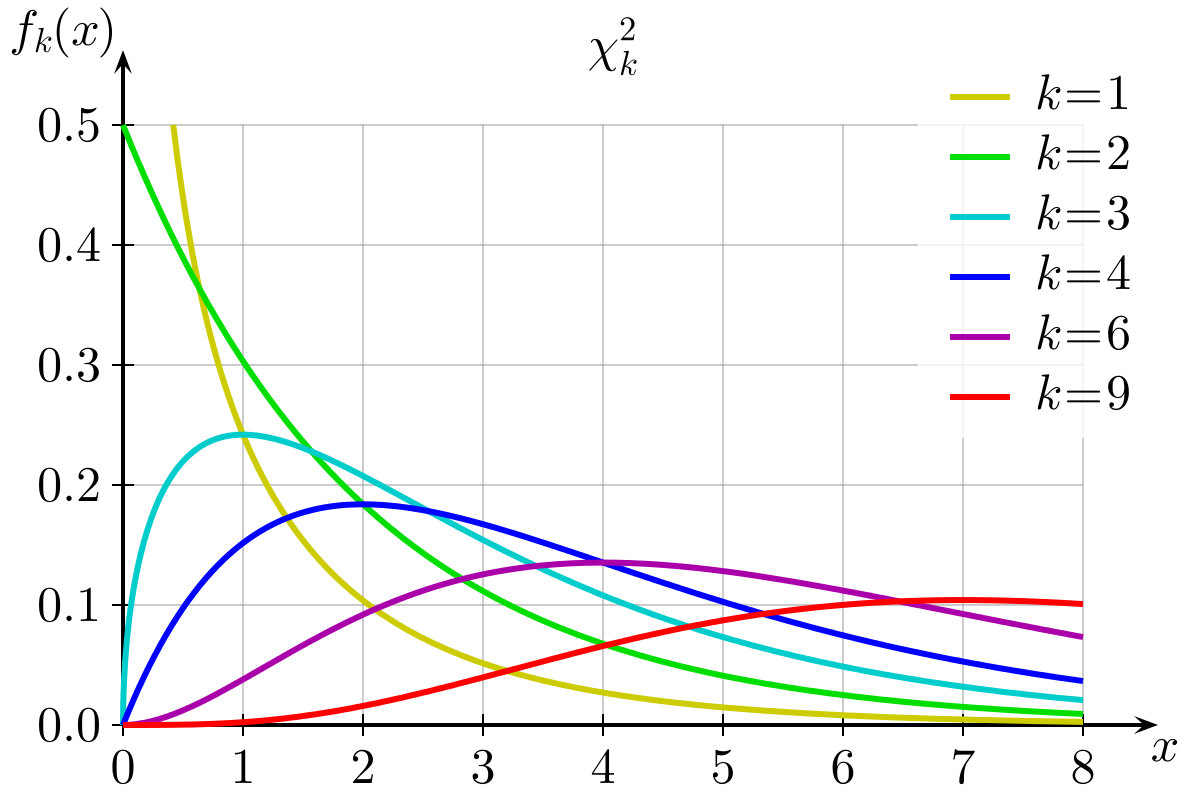
- 기댓값: E(X) = k
- 분산: V(X) = 2k
F-분포
- 독립적인 𝑥² 분포가 있을 때, 두 확률변수으 비
- 모집단 분산이 서로 동일하다고 가정되는 두 모집단으로부터 표본 크기가 각각 n₁, n₂인 독립적인 2개의 표본을 추출하였을 때 2개의 표본분산 s₁², s₂²의 비율 (s₁²/s₂²)
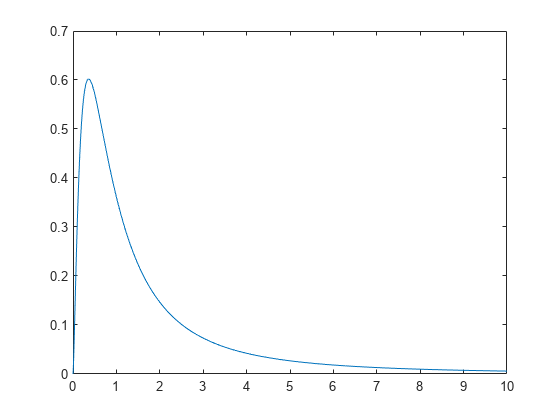
- 기댓값: E(X) = ${\frac {d_{2}}{d_{2}-2}}!$
- 분산: V(X) = ${\frac {2\,d_{2}^{2}\,(d_{1}+d_{2}-2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)}}!$