Article 4. 표본분포 2314

Section 1. 기술 통계

Paragraph 1. 표본 분포(Sampling Distribution) 개념

• 표본 분포란 모집단에서 추출한 크기가 일정한(n개인) 표본이 가지는 추정량의 확률 분포이다.

  

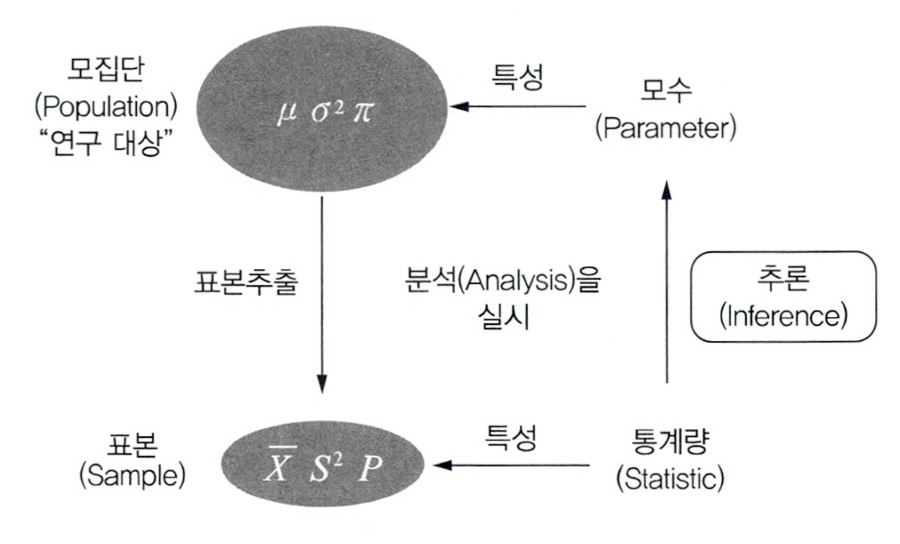
• 통계량에 의해 모집단에 있는 모수를 추론한다.

Paragraph 2. 표본 분포

Subparagraph 1. 표본 분포 용어

표본 분포의 용어로는 모집단, 모수, 통계량, 추정량, 표준편차 등이 있다.

용어	설명
모집단 (Population)	• 정보를 얻고자 하는 대상이 되는 집단 전체
모수 (Parameter)	• 모집단의 특성을 나타내는 대푯값
통계량 (Statistic)	• 표본에서 얻은 평균이나 표준 오차와 같은 값 • 이 값을 통해 모수를 추정하며, 무작위로 추출할 경우 각 표본에 따라 달라지는 확률변수
추정량 (Estimator)	• 모수의 추정을 위해 구해진 통계량
표준 편차 (Standard Deviation)	• 자료의 변동 정도 • σ, s를 의미
표준 오차 (Standard Error)	• 통계량의 변동 정도를 의미 • 평균을 낸 값들의 표준편차를 표준 오차라고 부름 • σ_x, s_x로 표기(보통은 X 위에 bar가 있는 형태로 표기

Subparagraph 2. 표본조사 용어

• 수집된 자료를 토대로 모집단의 특성을 추정하게 되는데, 이때 조사하는 모집단의 일부분을 표본(Sample)이라고 한다.
• 모집단의 일부분을 조사하는 행위가 표본조사이다.

구분	내용
표본오차 (Sampling Error)	• 모집단을 대표할 수 있는 표본 단위들이 조사대상으로 추출되지 못하기 때문에 발생하는 오차
비표본오차 (Non-Sampling Error)	• 표본오차를 제외한 모든 오차로써 조사 과정에서 발생하는 모든 부주의나 실수, 알 수 없는 원인 등 모든 오차를 의미하며 조사대상이 증가하면 오차가 커짐
표본편의 (Sampling Bias)	• 모수를 작게 또는 크게 할 때 추정하는 것과 같이 표본추출 방법에서 기인하는 오차 • 표본편의는 확률화에 의해 최소화하거나 없애지는 못함

Paragraph 3. 표본 분포와 관련된 법칙

표본 분포와 관련된 법칙에 대표적으로 큰 수의 법칙, 중심 극한 정리가 있다.

법칙	설명
큰 수의 법칙 (Law Large Number)	• 데이터를 많이 뽑을수록(n이 커질수록) 표본평균의 분산은 0에 가까워짐 • 데이터의 퍼짐이 적어져 정확해짐
중심 극한 정리 (Central Limit Theorem)	• 표본의 개수가 커지면 모집단의 분포와 상관없이 표본 분포는 정규 분포에 근사

Paragraph 4. 표본 분포의 유형

표본 분포의 유형으로는 Z-분포, T-분포, 카이제곱 분포, F-분포 등이 있다.

유형	설명
Z-분포	• 표본 통계량이 표본 평균일 때, 이를 표준화(정규화)시킨 표본 분포 • 개념적으로 정규 분포와 동일하여, 정규 분포 평균의 해석에 많이 쓰이는 분포
T-분포	• 모집단이 정규 분포라는 정도만 알고, 모 표준편차는 모를 때 사용하는 표준 분포
카이제곱 분포	• k개의 서로 독립적인 표준 정규 확률변수를 각각 제곱한 다음 합해서 얻어지는 분포
F-분포	• 표본 통계량이 두 독립 표본에서 계산된 표본분산들의 비율일 때의 표본 분포