Article 1. 점 추정 2321

less than 1 minute read

Paragraph 1. 점 추정(Point Estimation) 개념

점 추정 조건으로는 불편성, 효율성, 일치성, 충족성 등이 있다.

조건	설명
불편성(Unbiasedness)	모든 가능한 표본에서 얻은 추정량의 기댓값은 모집단의 모수와 차이가 없음
효율성(Efficiency)	추정량의 분산이 작을수록 좋음
일치성(Consistency)	표본의 크기가 아주 커지면, 추정량의 모수와 거의 같아짐
충족성(Sufficient)	추정량은 모수에 대하여 모든 정보를 제공

점 추정에 사용되는 통계는 표본평균, 표본분산, 중위수, 최빈값이 있다.

표본평균(Sample Mean)
- 모집단의 평균(모평균)을 추정하기 위한 추정량, 확률표본의 평균값
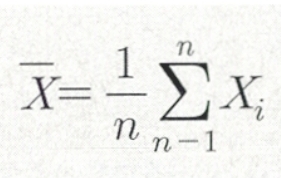
표본분산(Sample Variance)
- 모집단의 분산(모분산)을 추정하기 위한 추정량
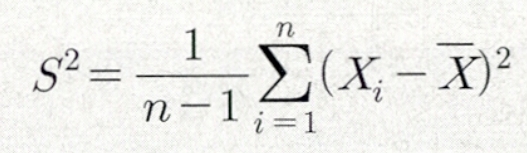
중위수(Median)
- 데이터를 크기 순서로 정렬하였을 때 가장 가운데 위치한 값
  
  예) 3, 5,7, 11, 13 경우에 n = 5이므로 (5+1)/2 = 3번째 값인 7이 중위수
최빈값(Mode)
- 주어진 데이터 중에서 가장 많이 관측되는 수
  
  예) 주어진 데이터가 3, 5, 9, 4, 5 경우에 가장 많이 관측된 5가 최빈값