Article 3. 가설검정 2323
Section 2. 추론 통계
Paragraph 1. 가설
Subparagraph 1. 가설(Hypothesis) 개념
- 가설이란 모집단의 특성, 특히 모수에 대한 가정 혹은 잠정적인 결론이다.
- 가설을 검정하기 위해 알고 싶은 내용을 기술한 가설의 종류에는 귀무가설과 대립가설이 있다.
Subparagraph 2. 가설의 종류
대표적인 가설의 종류로는 귀무가설과 대립가설이 있다.
-
귀무가설(H₀) (Null Hypothesis)
-
현재까지 주장되어 온 것이거나 기존과 비교하여 변화 혹은 차이가 없음을 나타내는 가설
예) 두통약 A와 B 간의 효과 차이가 없다.
-
-
대립가설(H₁) (Alternative Hypothesis)
-
표본을 통해 확실한 근거를 가지고 입증하고자 하는 가설
-
연구가설(Research Hypothesis)이라고 함
예) 두통약 A와 B간의 효과 차이가 존재한다.
-
Paragraph 2. 가설검정
Subparagraph 1. 가설검정(Statistical Hypothesis Test) 개념
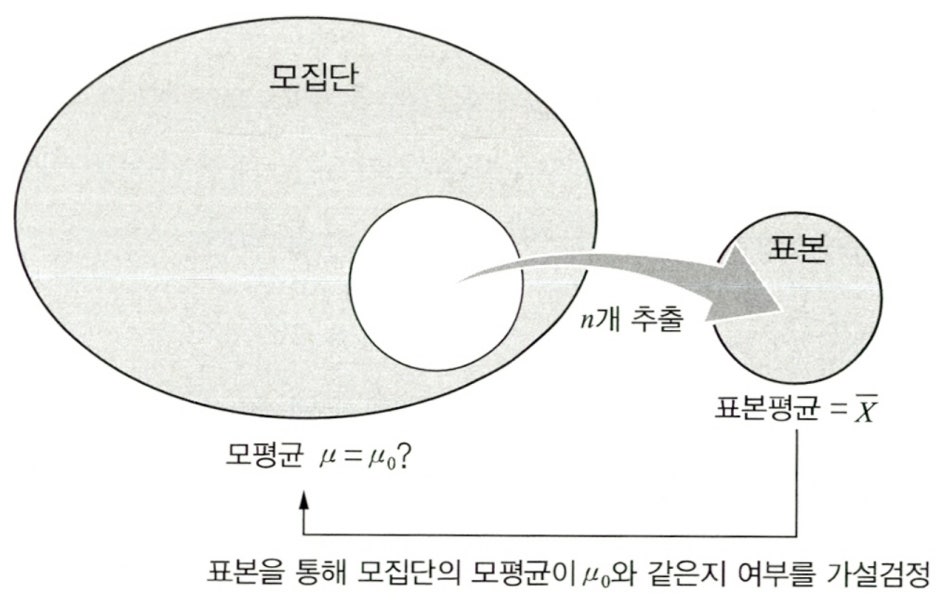
- 가설검정이란 모집단에 대한 통계적 가설을 세우고 표본을 추출한 다음, 그 표본을 통해 얻은 정보를 이용하여 통계적 가설의 진위를 판단하는 과정이다.
- 표본을 활용하여 모집단에 대입해보았을 때 새롭게 제시된 대립가설이 옳다고 판단할 수 있는지를 평가하는 과정이다
Subparagraph 2. 가설검정 절차
- 가설검정 시 p-값과 유의수준을 비교하여 귀무가설 혹은 대립가설을 채택하는 절차를 거치게 된다.
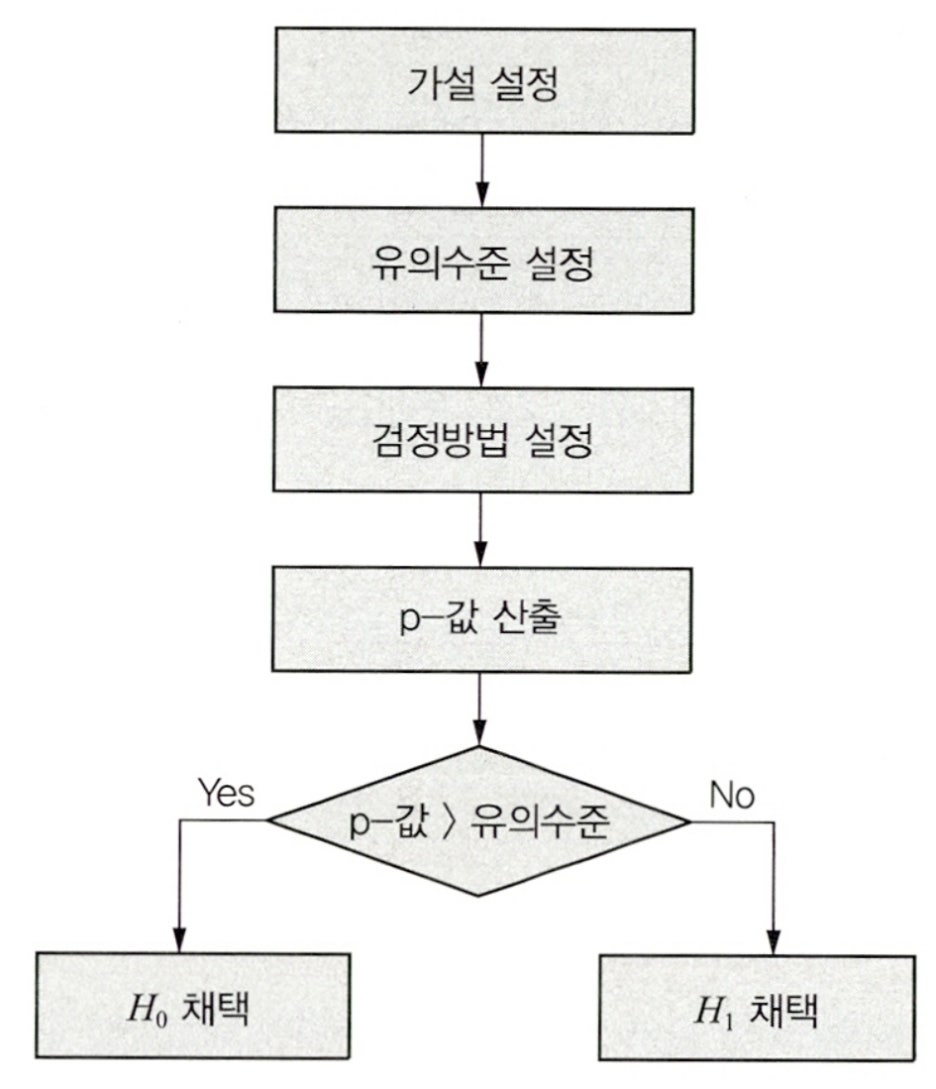
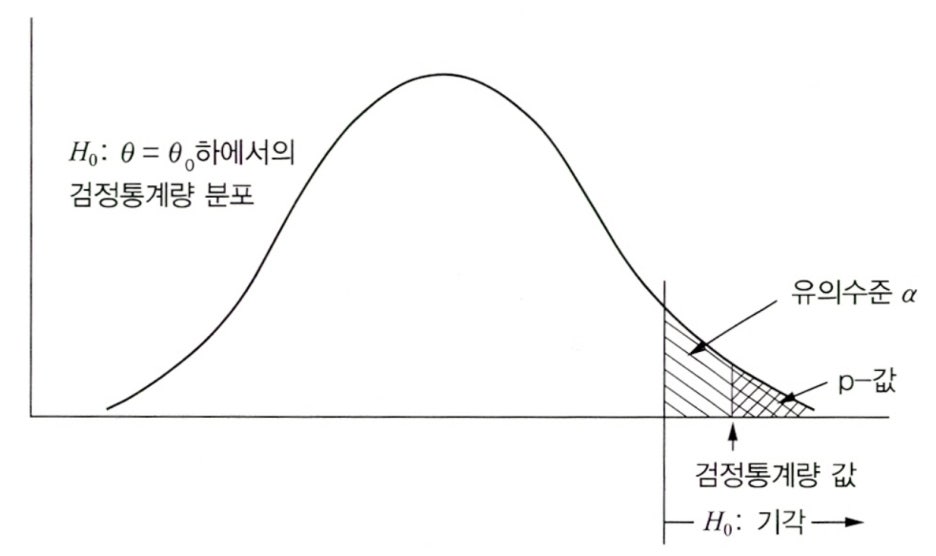
- p-값은 귀무가설이 참이라는 전제하에서 구한 검정 통계량의 값이 나타날 가능성으로 해석할 수 있으며, p-값이 유의수준보다 작으면(즉, 검정 통계량의 값이 나타날 가능성이 작으면) 귀무가설을 기각하고 대립가설을 채택하게 되며, p-값이 유의수준보다 크면 귀무가설을 채택하게 된다.
Subparagraph 3. 가설검정 방법
일반적으로 가설검정 방법은 대립가설의 형태에 따라서 양측검정과 단측검정이있다.
| 검정 | 설명 |
|---|---|
| 양측검정 | • 모수 θ(혹은 모수들의 함수)에 대해 표본자료를 바탕으로 모수가 특정 값 θ₀과 통계적으로 같은지 여부를 판단 • 귀무가설을 H₀: θ = θ₀, 대립가설을 H₁: θ ≠ θ₀와 같이 설정 |
| 단측검정 | • 모수 θ(혹은 모수들의 함수)에 대해 표본자료를 바탕으로 모수가 특정 값 θ₀과 통계적으로 큰지 작은지 여부를 판단 • 귀무가설이 H₀: θ ≧ θ₀일 경우, 대립가설을 H₁: θ < θ₀와 같이 설정 • 귀무가설이 H₀: θ ≦ θ₀일 경우, 대립가설을 H₁: θ > θ₀와 같이 설정 |
Paragraph 3. 가설검정의 오류
Subparagraph 1. 가설검정 오류의 개념
통계적인 방법에 근거하여 주어진 가설을 검증하는 데 있어 모집단 전체를 통해 검증하는 것이 아닌 모집단으로부터 추출된 표본을 기반으로 모집단에 대한 결론을 내리는 것이기 때문에 다음과 같은 통계적인 오류가 발생할 가능성이 항상 존재한다.
Subparagraph 2. 가설검정 오류의 종류
- 가설검정 오류의 종류로는 제1종 오류, 제2종 오류가 있다.
-
제1종 오류
- 귀무가설이 참인데 잘못하여 이를 기각하게 되는 오류
- 유의수준(Level of Significance)
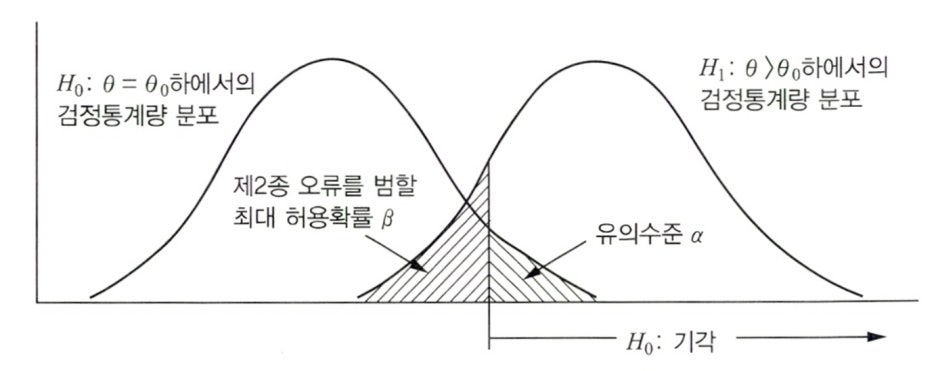
- 제1종 오류를 범할 최대 허용확률을 의미 α로 표기
- 신뢰수준(Level of Confidence)
- 귀무가설이 참일 때 이를 참이라고 판단하는 확률 (1 - α)
-
제2종 오류
- 귀무가설이 참이 아닌데 잘못하여 이를 채택하게 되는 오류
- 베타 수준(β Level)
- 제2종 오류를 범할 최대 허용확률을 의미 β로 표기
- 검정력
- 귀무가설이 참이 아닌 경우 이를 기각할 수 있는 확률 (1 - β)
- 일반적으로 1종 오류의 영향이 2종 오류의 영향보다 크므로, 유의수준(α)을 기준으로 가설검정을 수행한다.

Paragraph 4. 검정 통계량
- 검정 통계량은 가설검정의 대상이 되는 모수를 추론하기 위해 사용되는 표본 통계량이다.
- 귀무가설이 참이라는 전제하에서 모집단으로부터 추출된 확률표본의 정보를 이용하여 계산된다.
Paragraph 5. p-값
- 귀무가설이 참이라는 가정에 따라 주어진 표본 데이터를 희소 또는 극한값으로 얻을 확률값을 p-값이라고 한다.
- 검정 통계량 및 이의 확률분포에 근거하여 귀무가설이 참일 때 귀무가설을 기각하게 되는 제1종 오류를 범할 확률로도 볼 수 있다.