Article 1. 회귀 분석 3211
Section 1. 분석기법
Paragraph 1. 회귀 분석(Regression Analysis) 개념
- 회귀 분석은 하나 이상의 독립변수들이 종속변수에 미치는 영향을 추정할 수 있는 토계기법이다.
- 변수들 사이의 인과관계를 밝히고 모형을 적합(Fit)하여 관심 있는 변수를 예측하거나 추론하기 위한 분석 방법이다.
Subparagraph 1. 회귀 분석 변수
회귀 분석에서 사용되는 변수는 결과에 영향을 주는 변수인 독립변수와 독립변수에 의해 영향을 받는 종속변수로 구분을 할 수가 있으며 다양한 다른 이름으로 명명된다.
| 변수 구분 | 변수명 |
|---|---|
| 영향을 주는 변수(x) | 독립변수(Indepoendent Variable), 설명변수(Explanatory Variable), 예측변수(Predictor Variable)라고 명명될 수 있음 |
| 영향을 받는 변수(y) | 종속변수(Dependent Variable), 반응변수(Response Variable), 결과변수(Outcome Variable)라고 명명될 수 있음 |
Subparagraph 2. 회귀 모형 가정 및 검증
- 데이터가 선형성, 독립성, 등분산성, 비상관성, 정상성의 가정을 만족시킬 수 있어야 한다.
| 가정 | 설명 |
|---|---|
| 선형성 | • 독립변수의 변화에 따라 종속변수도 일정 크기로 변화 • 독립변수와 종속변수의 관계의 형태는 선형 |
| 독립성 | • 잔차와 독립변수의 값이 관련돼 있지 않음 |
| 등분산성 | • 독립변수의 모든 값에 대해 오차들이 분산이 일정 |
| 비상관성 | • 관측치들의 잔차들끼리 상관이 없어야 함 |
| 정상성 | • 잔차항이 정규 분포를 이뤄야 함 |
- 회귀 모형 가정에 적합한지 검증한다.
⬇회귀 모형 가정 검증
| 모형 | 설명 |
|---|---|
| 단순선형 회귀 분석 | • 독립변수와 종속변수 간의 선형성 검증 • 선형성 검증을 위해 산점도 활용 |
| 다중선형 회귀 분석 | • 회귀 모형 가정인 선형성, 독립성, 등분산성, 비상관성, 정상성을 모두 만족하는지 검증 |
Subparagraph 3. 회귀 모형 검증
적합한 모형을 선택한 후에는 모형이 적절한지 확인한다.
⬇회귀 모형 검증 체크리스트
| 체크리스트 | 설명 |
|---|---|
| 모형이 통계적으로 유의미한가? | • F-통계량 확인 • 유의수준 5% 하에서 F-통계량의 p-값이 0.005보다 작으면 추정된 회귀식은 통계적으로 유의하다고 볼 수 있음 |
| 회귀계수들이 유의미한가? | • 해당 계수의 T-통계량과 p-값 또는 이들의 신뢰구간 확인 |
| 모형이 얼마나 설명력을 갖는가? | • 결정계수를 확인, 결정계수는 0~1값을 가지며, 높은 값을 가질 수록 추정된 회귀식의 설명력이 높다. |
| 모형이 데이터를 잘 적합하고 있는가? | • 잔차를 그래프로 그리고 회귀진단을 한다. |
| 데이터가 가정을 만족시키는가? | • 선형성, 독립성, 등분산성, 정상성 가정을 만족시켜야 함 |
Paragraph 2. 회귀 분석 유형
회귀 분석은 독립변수 및 종속변수의 개수 및 특성에 따라 단순회귀, 다중회귀, 다항회귀, 곡선회귀, 로지스틱 회귀, 비선형 회귀와 같이 분류한다.
| 종류 | 모형 |
|---|---|
| 단순회귀 | • 독립변수가 1개이며, 종속변수와의 관계가 직성 |
| 다중회귀 | • 독립변수가 K개이며 종속변수와의 관계가 선형(1차 함수) |
| 다항회귀 | • 독립변수와 종속변수와의 관계가 1차 함수 이상인 관계(단, 독립변수가 1개일 경우에는 2차 함수 이상) |
| 곡선회귀 | • 독립변수가 1개이며, 종속변수와의 관계가 곡선 |
| 로지스틱회귀 | • 종속변수가 범주형(2진 변수)인 경우 적용 • 단순 로지스틱 회귀 및 다중, 다항 로지스틱 회귀로 확장 가능 |
| 비선형 회귀 | • 회귀식의 모양이 미지의 모수들의 선형관계로 이뤄져 있지 않은 모형 |
Subparagraph 1. 단순선형 회귀 분석(Simple Linear Regression Analysis)
Clause 1. 단순선형 회귀식
- 단순선형 회귀 모형은 회귀 모형 중에서 가장 단순한 모형이다.
- 독립변수와 종속변수가 각각 한 개이며 오차항이 있는 선형관계로 이뤄져 있다.
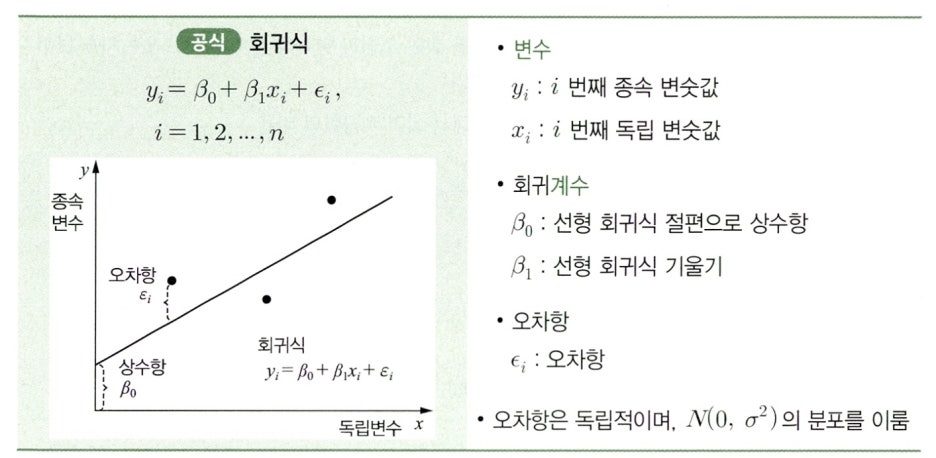
Clause 2. 회귀계수의 추정
- 회귀계수는
최소제곱법을 사용하여 추정한다. - 최소제곱법이란 측정값을 기초로 하여 제곱합을 만들고 그것을 최소로 하는 값을 구하여 측정결과를 처리하는 방법으로 오차 제곱의 합이 가장 작은 해를 구하는 것을 의미한다.

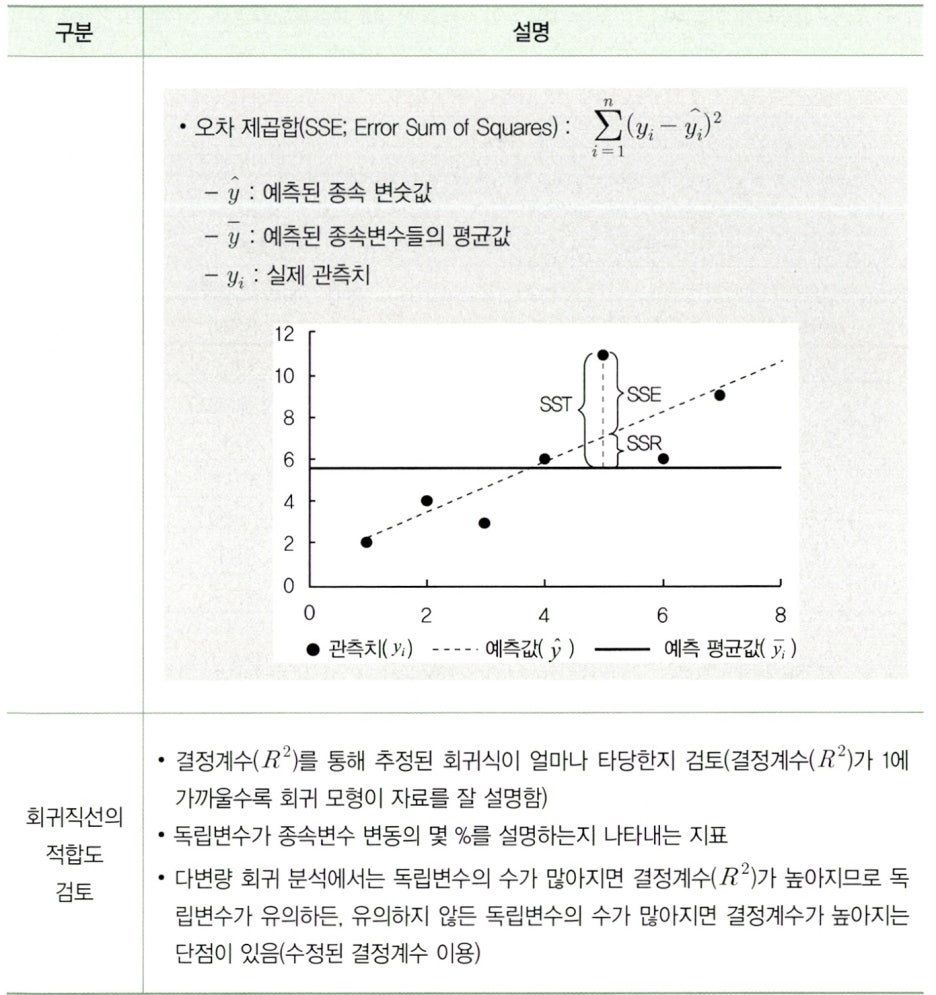
Clause 3. 회귀 분석의 검정
회귀 분석 결과가 적합한지 아래와 같이 검증한다.

Subparagraph 2. 다중선형 회귀 분석(다변량 회귀 분석; Multi Linear Regression Analysis)
Clause 1. 다중선형 회귀 분석 회귀식

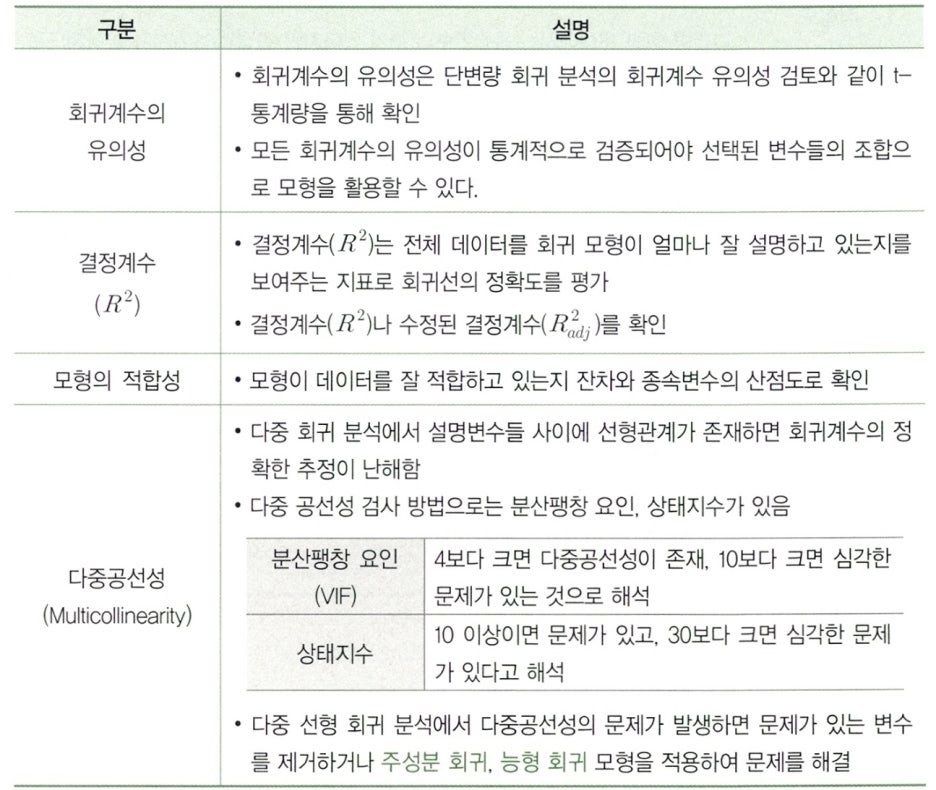
Clause 2. 모형의 통계적 유의성
- 모형의 통계적 유의성은 F-통계량으로 확인한다.
- 융의수준 5% 하에서 F-통계량의 p-값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의하다고 볼 수 있다.
- n은 표본의 개수고 k는 변수의 개수일 때 F-통계량은 아래와 같이 구할 수 있다.
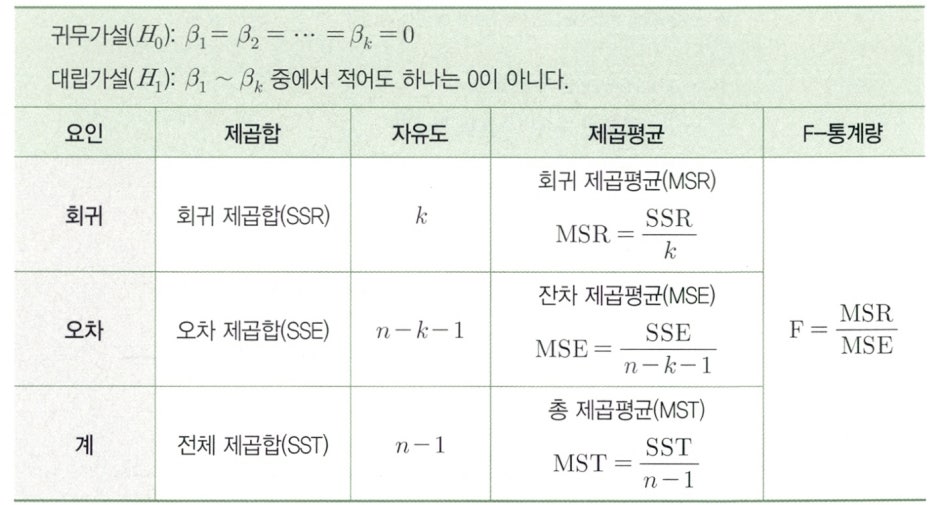
- F-통계량이 크면 p-값이 0.05보다 작아지고 이렇게 되면 귀무가설을 기각하므로 모형이 유의하다고 결론 지울 수 있다.
Paragraph 3. 최적 회귀방정식의 선택
모든 가능한 독립변수들의 조합에 대한 회귀 모형을 생성한 뒤 가장 적합한 회귀 모형을 선택한다.
| 유형 | 설명 |
|---|---|
| 전진 선택법 (Forward Selection) |
절편만 있는 상수 모형부터 시작해 중요하다고 생각되는 설명변수를 차례로 모형에 추가하는 방식 |
| 후진 제거법 (Backward Elimination) |
독립변수 후보 모두를 포함한 모형에서 출발해 제곱합의 기준으로 가장적은 영향을 주는 변수부터 하나씩 제거하면서 더 이상 유의하지 않은 변수가 없을 때까지 설명변수들을 제거하고 이때의 모형을 선택하는 방법 |
| 단계적 방법 (Stepwise Method) |
변수를 추가하면서 새롭게 추가된 변수에 기인해 기존 변수가 그 중요도가 약화되면 해당 변수를 제거하는 단계별 추가 또는 제거되는 변수의 여부를 검토해 더 이상 없을 때 중단하는 방법 |
Paragraph 4. 단순선형 회귀 분석(Regression Analysis) 코드 해석
| 함수 및 용어 | 설명 |
|---|---|
| lm() | • 단순 회귀 모형을 수행하는 함수 |
| Residual | • 예측하고자 하는 변수의 실젯값과 회귀 분석으로 얻어진 값 사이에서 표준 오차로 인해 발생한 차이 |
| Coefficients | • 회귀 모형에서 사용되는 회귀계수 • 회귀 분석에 의해 계산된 절편(Intercept)과 각 독립변수(x)의 기울기 값 |
| Significance stars(*) | • 계산된 p-값에 따라 별표로 나타내는 중요도 수준 • ***는 높은 중요도, *는 낮은 중요도를 의미 |
| Multiple R-squared | • 결정계수(R²) • 모델에 의하여 해석되는 예측의 변동량으로, 모델의 적합성을 평가하는 척도로도 사용 • 1이 최고치이므로 1에 가까운 값이 최적 모델임 |
| Adjusted R-squared | • 수정된 결정계수 |
| F-statistic | • F-통계량 |
| DF | • 자유도(Degree of Freedom) • 샘플에 포함된 관측치의 개수와 모델에 사용된 변수 개수와의 차이 |
| p-value | • 유의수준으로 p-값이 작을수록 신뢰구간에 포함됨 |
