Article 3. 의사결정나무 3213
Section 1. 분석기법
Paragraph 1. 의사결정나무(Decision Tree) 개념
- 데이터들이 가진 속성들로부터 분할 기준 속성을 판별하고, 분할 기준 속성에 따라 트리 형태로 모델링하는 분류 예측 모델이다.
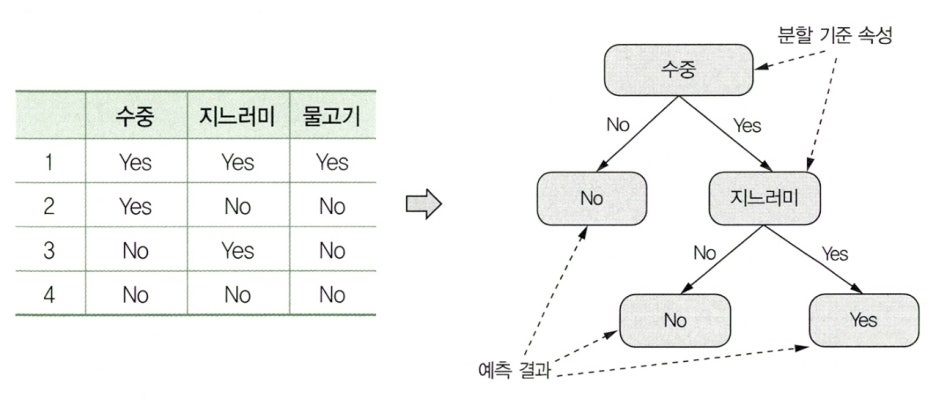
- 의사결정나무 기법은 분석의 대상을
분류함수를 활용하여 의사결정 규칙으로 이루어진 나무 모양으로 그리는 기법이다. - 의사결정나무 구조는 연속적으로 발생하는 의사결정 문제를 시각화해서 의사결정이 이루어지는 시점과 성과 파악을 쉽게 해준다.
- 의사결정나무 기법의 해석이 용이한 이유는 계산 결과가 의사결정나무에 직접적으로 나타나기 때문이다.
Paragraph 2. 의사결정나무의 구성요소
의사결정나무는 뿌리 마디, 자식 마디, 부모 마디, 끝마디, 중간 마디, 가지, 깊이 등의 요소로 구성되어 있다.
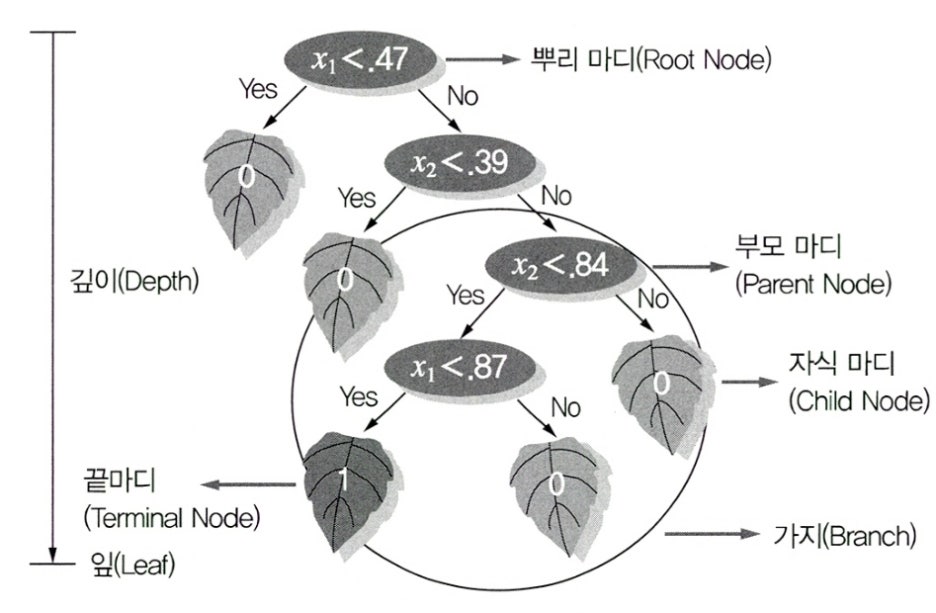
| 구성요소 | 설명 |
|---|---|
| 부모 마디 (Parent Node) |
• 주어진 마디의 상위에 있는 마디 |
| 자식 마디 (Child Node) |
• 하나의 마디로부터 분리되어 나간 2개 이상의 마디들 |
| 뿌리 마디 (Root Node) |
• 시작되는 마디로 전체 자료를 포함 |
| 끝마디 (Terminal Node) |
• 잎(Leaf) 노드라고도 불림 • 자식 마디가 없는 마디 |
| 중간 마디 (Internal Node) |
• 부모 마디와 자식 마디가 모두 있는 마디 |
| 가지 (Branch) |
• 뿌리 마디로부터 끝마디까지 연결된 마디들 |
| 깊이 (Depth) |
• 뿌리 마디부터 끝마디까지의 중간 마디들의 수 |
Paragraph 3. 해석력과 예측력
- 은행에서 신용평가에서는 평가 결과 부적격 판정이 나온 경우 대상자에게 부적격 이유를 설명해야 하지 때문에 의사결정나무의 해석력에 집중한다.
- 기대 집단의 사람들 중 가장 크고, 많은 반응을 보일 상품 구매 고객의 모집방안을 예측하고자 하는 경우에 의사결정나무의 예측력에 집중한다.
Paragraph 4. 의사결정나무의 분석
Subparagraph 1. 의사결정나무의 분석 과정
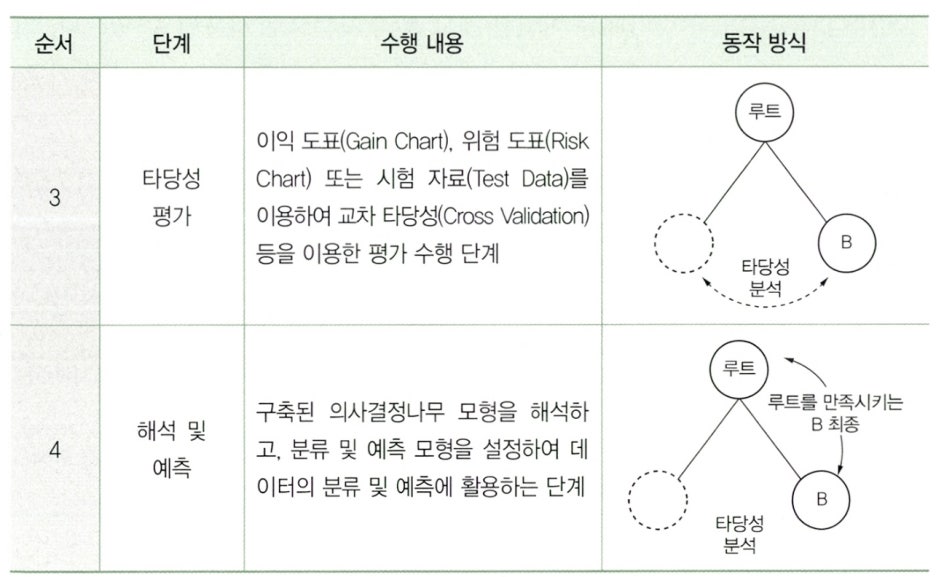
Subparagraph 2. 의사결정나무의 성장
- 학습자료를 (x_j, y_j) j = 1, 2, 3, 4, ⋅⋅⋅, n 으로 나타내면 x_j = (x_j1, ⋅⋅⋅, x_jp)이다.
- 의사결정나무에서 나무 모형의 성장 과정은 x들로 이루어진 입력 공간을 재귀적으로 분할하는 과정이라고 할 수 있다.
Clause 1. 분류 규칙(Splitting Rule)
- 의사결정나무에서 분리변수(Split Variable)가 연속형인 경우, A = x_i ≤ s 이다.
- 의사결정나무에서 분리 변수가 범주형{1, 2, 3, 4}인 경우에는, A = 1, 2, 4와 Aᶜ = 3으로 나눌 수 있다.
- 의사결정나무에서 최적 분할의 결정은 불순도 감소량을 가장 크게 하는 분할이다.
- 각 단계에서 최적 분리 기준에 의한 분할을 찾은 후 각 분할에 대해서도 동일한 과정을 반복한다.
Clause 2. 분리 기준(Splitting Criterion)
- 분리 기준은 하나의 부모 마디로부터 자식 마디들이 형성될 때, 입력변수(Input Variable)의 선택과 범주(Category)의 병합이 이루어질 기준을 의미한다.
- 어떤 입력변수를 이용하여 어떻게 분리하는 것이 목표변수의 분포를 가장 잘 구별해주는지를 파악하여 자식 마디가 형성되는데, 목표변수의 분포를 구별하는 정도를
순수도, 또는 불순도(Impurity)에 의해서 측정하는 것이다. - 의사결정나무는 부모 마디의 순수도에 비해서 자식 마디들의 순수도가 증가하도록 자식 마디를 형성해나가게 된다.
- 마디의 순수도를 나타내는 어떠한 것도 분리 기준으로 사용될 수 있으나, 일반적으로는 목표변수의 측도에 따라서 이산형 목표변수에 사용되는 분리 기준과 연속형 목표변수에 사용되는 분리 기준이 사용된다.
⬇이산형 목표변수에 사용되는 분리 기준
| 기준값 | 분리 기준 |
|---|---|
| 카이제곱 통계량의 p-값 | p-값이 가장 작은 예측변수와 그 당시의 최적 분리를 통해서 자식 마디 형성 |
| 지니 지수 (Gini Index) |
불순도를 측정하는 하나의 지수로도 지니 지수를 가장 감소시켜주는 예측변수와 그 당시의 최적 분리를 통해서 자식 마디 선택 |
| 엔트로피 지수 (Entropy Index) |
엔트로피 지수가 가장 작은 예측변수와 그 당시의 최적 분리를 통해서 자식 마디를 형성 |
⬇연속형 목표변수에 사용되는 분리 기준
| 기준값 | 분리 기준 |
|---|---|
| 분산 분석에서 F-통계량 | p-값이 가장 작은 예측변수와 그 당시의 최적 분리를 통해서 자식 마디 형성 |
| 분산의 감소량 | 예측 오차를 최소화하는 것과 같은 기준으로 분산의 감소량을 최대화하는 기준의 최적 분리를 통해서 자식 마디 형성 |
Clause 3. 정지 규칙(Stopping Rule)
- 의사결정나무에서 정지 규칙과 가지치기라는 순서가 있는데 정지 규칙은 더 이상 분리가 일어나지 않고 현재의 마디가 끝마디가 되도록 하는 규칙이다.
- 정지기준(Stopping Criterion)은 의사결정나무의 깊이(Depth)를 지정, 끝마디의 레코드 수의 최소 개수를 지정한다.
Subparagraph 3. 나무의 가지치기(Pruning)
- 의사결정나무에서 너무 큰 나무 모형은 자료를
과대 적합하고, 너무 작은 나무 모형은과소 적합할 위험성이 있다. - 의사결정나무의 크기를 모형의 복잡도로 볼 수 있으며 최적의 나무 크기는 대상 자료로부터 추정하게 된다.
- 일반적으로 사용되는 방법은 마디에 속하는 자료가 일정 수 (10을 예로 든다면) 이하일 때 분할을 멈추고 비용ㅡ복잡도 가지치기(Cost Complexity Pruning)를 활용하여 성장시킨 나무에 대한 가지치기를 한다.
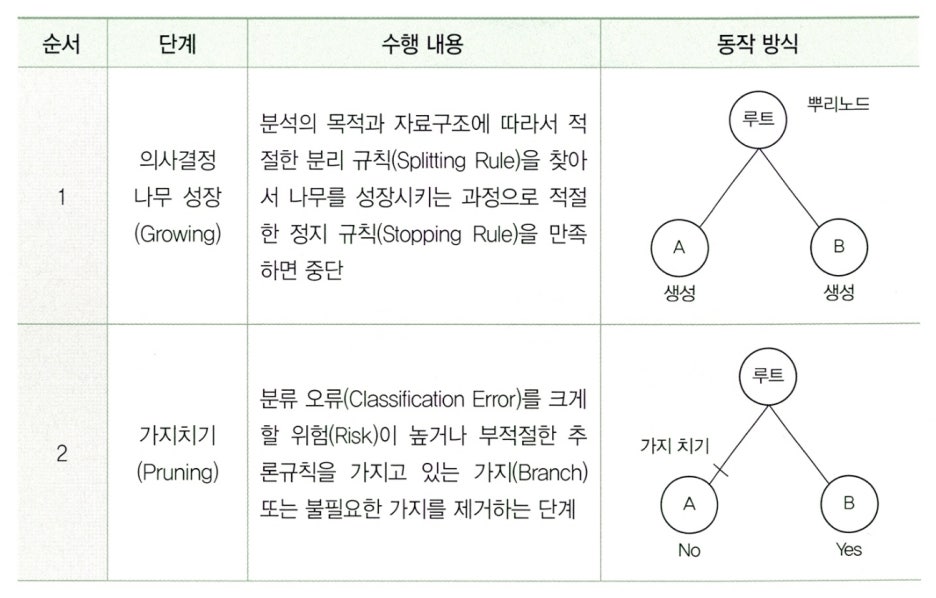
Paragraph 5. 불순도의 여러 가지 측도
목표변수가 범주형 변수인 의사결정나무의 분류 규칙을 선택하기 위해서는 카이제곱 통계량, 지니 지수, 엔트로피 지수 활용한다.
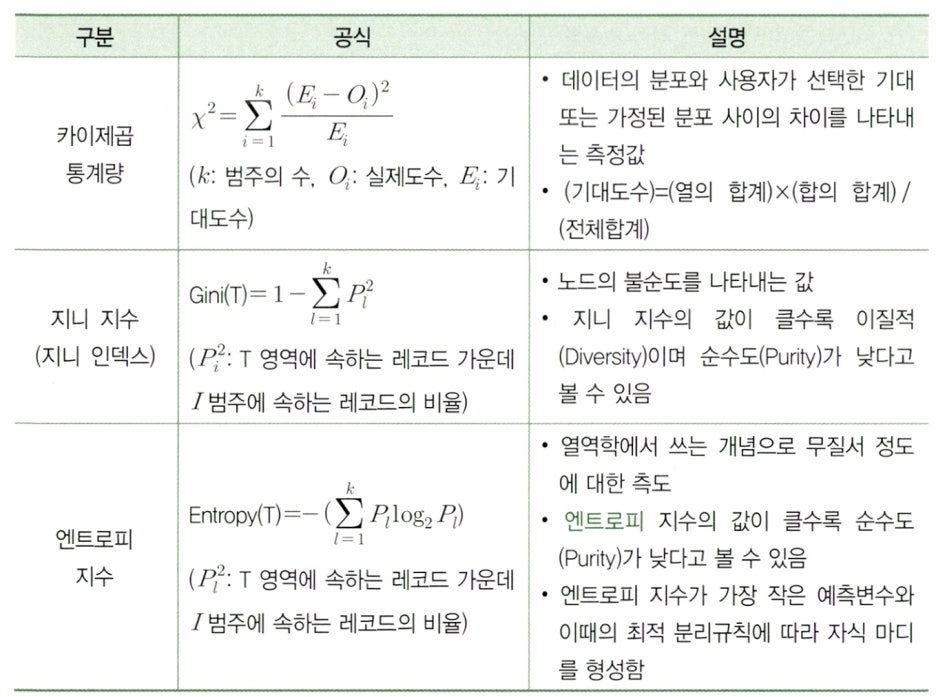
카이제곱 통계량 구하기
지니 지수 구하기
엔트로피 지수 구하기
Paragraph 6. 불순도의 여러 가지 측도
⬇의사결정나무 알고리즘
| 구분 | 설명 |
|---|---|
| CART (Classification And Regression Tree) |
• CART 기법은 각 독립변수를 이분화하는 과정을 반복하여 이진트리 형태를 형성함으로써 분류를 수행하는 방법이다 • 가장 널리 사용되는 의사결정나무 알고리즘 • 가장 성취도가 좋은 변수 및 수준을 찾는 것에 중점 • 불순도의 측도로 출력(목적) 변수가 범주형일 경우는 지니 지수를 이용, 연속형일 경우는 분산을 이용한 이진 분리(Binary Split)를 이용 • 개별 입력변수뿐만 아니라 입력변수들의 선형 결합 중에서 최적의 분리를 구할 수 있음 |
| C4.5와 C5.0 | • 가지치기를 사용할 때 학습자료를 사용 • 목표변수가 반드시 범주형이어야 하며, 불순도의 측도로는 엔트로피 지수(Entropy index) 사용 • CART와 다르게 각 마디에서 다지 분리(Multiple Split)가 가능하며 범주형 입력변수에 대해서는 범주의 수만큼 분리가 일어남 |
| CHAID(Chi-squared Automatic Interaction Detection) | • AID(Automatic Interaction Detection)를 발전시킨 알고리즘 • 가지치기하지 않고 나무를 적당한 크기에서 성장을 중지하며 입력변수가 반드시 범주형 변수형이어야 함 • 불순도의 측도로는 카이제곱 통계량을 사용 • 분리 방법은 다지 분리(Multiple Split) 사용 • 분리 변수의 각 범주가 하나의 부 마디(Sub-Node)를 형성 |
| QUEST | • 변수의 선택에서 범주의 개수가 많은 범주형 변수로의 편향이 심각한 CART의 문제점을 개선한 알고리즘• 변수 선택 편향(Bias)이 거의 없음 • 분리 규칙은 분리 변수 선택과 분리점 선택의 두 단계로 나누어 시행 • 붌순도의 측도로는 카이제곱 통계량을 사용 • 분리 방법은 이진 분리(Binary Split) 사용 |
⬇의사결정나무 알고리즘 요약표
| 구분 | CART | C5.0 | CHAID | QUEST |
|---|---|---|---|---|
| 목표변수 | • 범주형 • 연속형 |
• 범주형 | • 범주형 • 연속형 |
• 범주형 |
| 예측 변수 | • 범주형 • 연속형 |
• 범주형 • 연속형 |
• 범주형 | • 범주형 • 연속형 |
| 분리 기준 | • 지니 지수 • 분산의 감소량 |
• 엔트로피 지수 | • 카이제곱 통계량 • F-검정 |
• 카이제곱 통계량 • F-검정 |
| 분리 방법 | • 이진 분리 | • 다지 분리 | • 다지 분리 | • 이진 분리 |
Paragraph 7. 불순도의 어러 가지 측도
의사결정나무는 주어진 입력값에 대하여 출력밧을 예측하는 모형으로 분류 나무와 회귀 나무 모형이 있다.
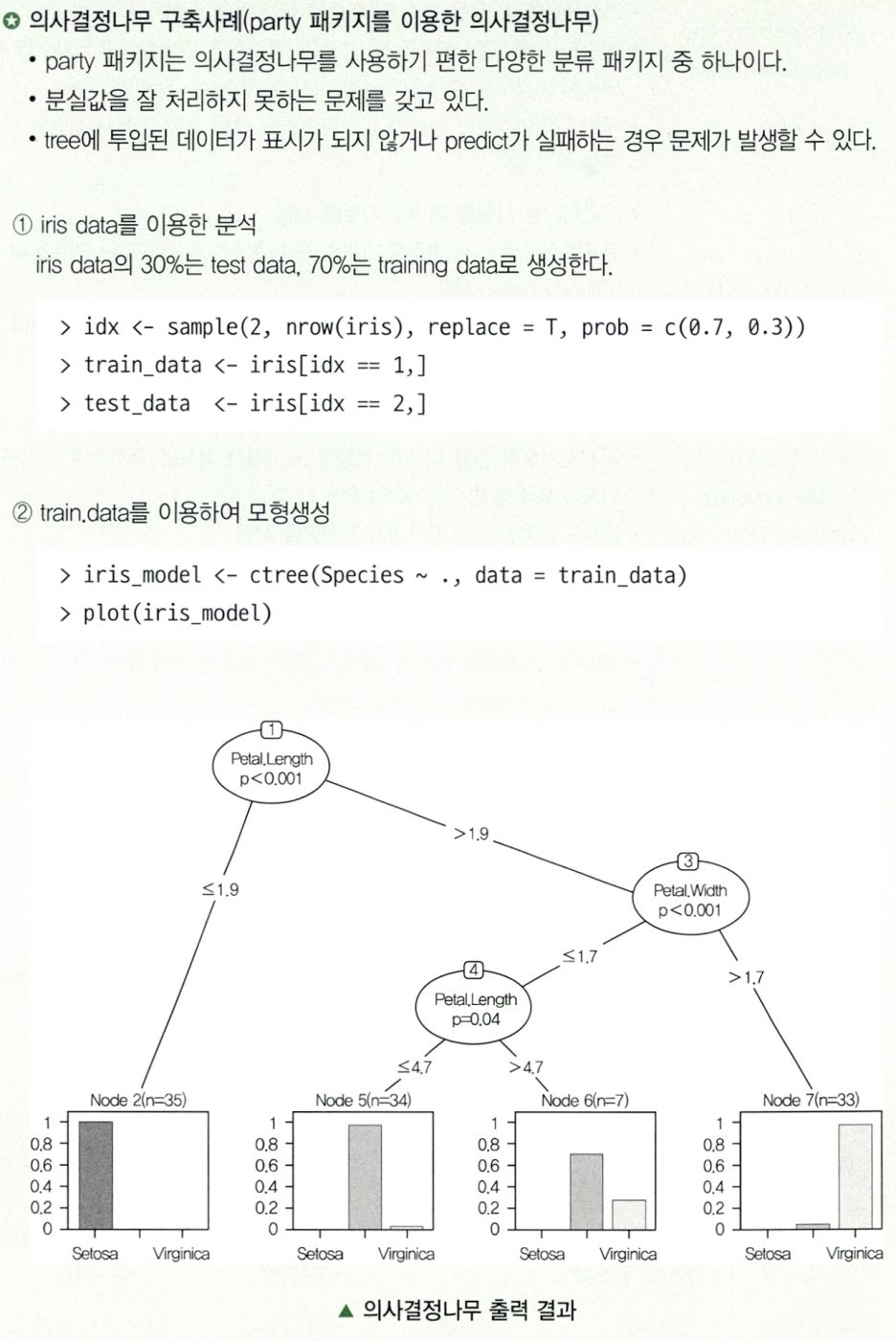
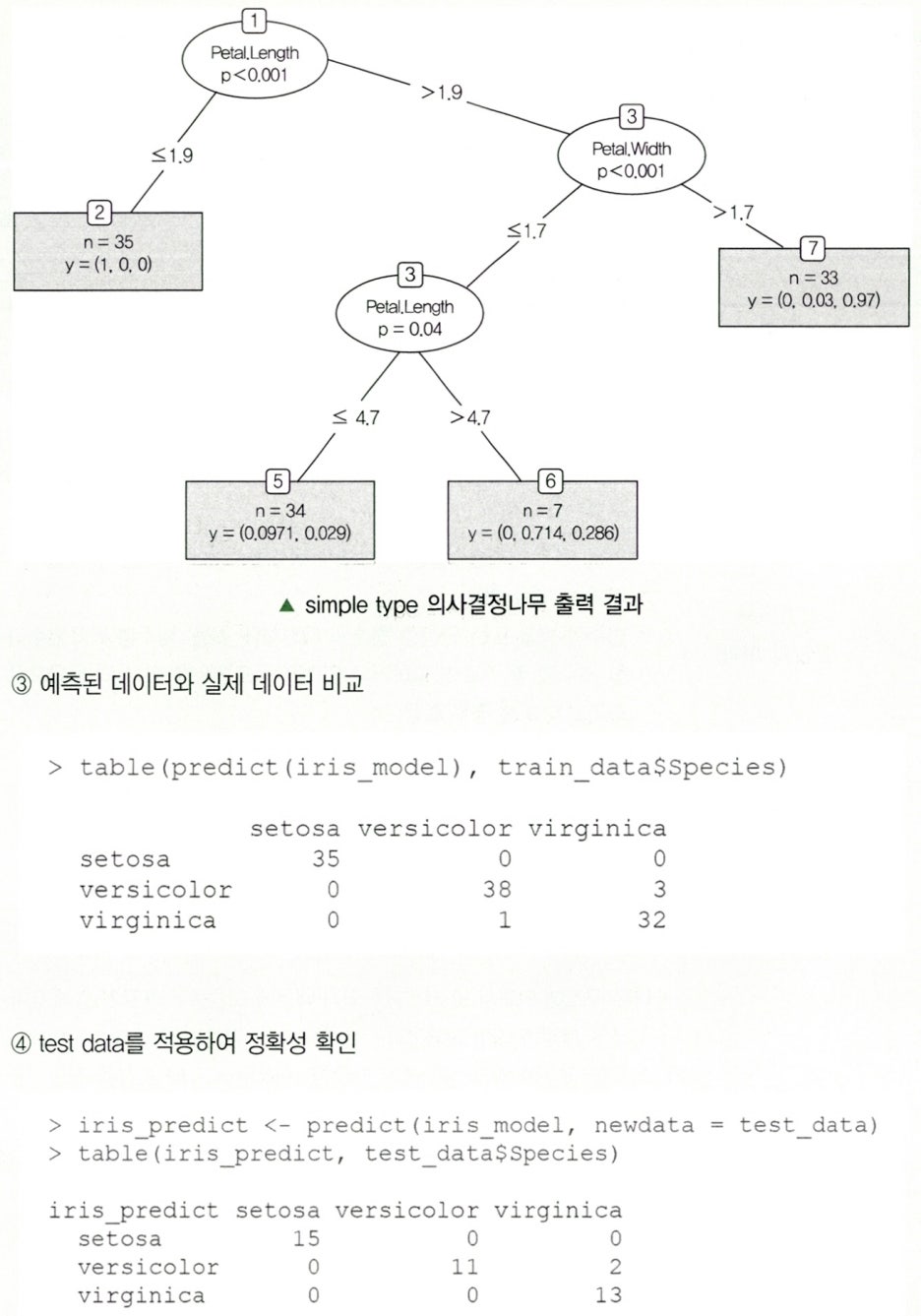
Paragraph 8. 의사결정나무의 활용 및 장단점
Subparagraph 1. 의사결정나무의 활용
| 활용용도 | 설명 |
|---|---|
| 세분화 | • 데이터를 비슷한 특성을 갖는 몇 개의 그룹으로 분할해서 그룹별 특성을 발견하고자 하는 경우 활용 |
| 분류 | • 여러 예측변수들에 근거해서 관측 개체의 목표변수 범주를 몇 개의 등급으로 분류하고자 하는 경우에 활용 |
| 예측 | • 자료에서 규칙을 찾아내고 이를 이용해서 미래의 사건을 예측하고자 하는 경우 활용 |
| 차원축소 및 변수 선택 | • 매우 많은 수의 예측변수 중에서 목표변수에 큰 영향을 미치는 변수들을 구분하고자 하는 경우에 활용 |
교호작용 효과와 파악 |
• 여러 개의 예측변수들을 결합해서 목표변수에 작용하는 규칙을 파악하고자 하는 경우 활용 • 범주의 병합 또는 연속형 변수의 이산화에 활용: 범줗형 목표변수의 범주를 소수의 몇 개로 병합하거나 연속형 목표변수를 몇 개의 등급으로 이산화하고자 하는 경우 활용 |
Subparagraph 2. 의사결정나무의 장단점
| 장점 | 설명 |
|---|---|
| 해석의 용이성 | • 나무 구조에 의해서 모형이 표현되기 때문에 모형을 사용자가 쉽게 이해 가능 • 새로운 개체에 대한 분류 또는 예측을 하기 위해서 뿌리 마디로부터 끝마디까지를 단순히 따라가가면 되기 때문에, 새로운 자료에 모형을 적합 시키기가 쉬움 • 나무 구조로부터 어떤 입력변수가 목표변수를 설명하기 위해서 더 중요한지를 쉽게 파악 가능 |
| 상호작용 효과의 해석 가능 | • 두 개 이상의 변수가 결합하여 목표변수에 어떻게 영향을 주는지 쉽게 파악 가능 • 의사결정나무는 유용한 입력변수나 상호작용(Interaction)의 효과 또는 비선형성(Nonlinearity)을 자동으로 찾아내는 알고리즘이라 할 수 있음 |
| 비모수적 모형 | • 의사결정나무는 선형성(Linearity)이나 정규성(Normality) 또는 등분산성(Equal Variance) 등의 가정을 필요로 하지 않는 비모수적인(Non-Parametric) 방법임 • 의사결정나무에서는 순서형 또는 연속형 변수는 단지 순위(Rank)만 분석에 영향을 주기 때문에 이상값에 민감하지 않다는 장점이 있음 |
| 유연성과 정확도가 높음 | • 대용량 데이터에서도 빠르게 만들 수 있음 • 설명변수나 목표변수에 수치형 변수와 범주형 변수를 모두 사용 가능 • 모형 분류 정확도가 높음 |
| 단점 | 설명 |
|---|---|
| 비연속성 | • 의사결정나무에서는 연속형 변수를 비연속적인 값으로 취급하기 때문에 분리의 경계점 근방에서는 예측 오류가 클 가능성이 있음 |
| 선형성 또는 주 효과의 결여 | • 선형모형(Linear Model)에서 주 효과(Main Effect)는 다른 예측변수와 관련시키지 않고서도 각 변수의 영향력을 해석할 수 있다는 장점을 가지고 있는데 의사결정나무에서는 선형(Linear) 또는 주 효과(Main Effect) 모형에서와 같은 결과를 얻을 수 없다는 한계점이 있음 |
| 비안정성 | • 학습용 자료(Training Data)에만 의존하는 의사결정나무는 새로운 자료의 예측에서 불안정(Unstable)하여 과대 적합이 발생할 가능성이 있음 • 분석용 자료의 크기가 너무 작은 경우와 너무 많은 가지를 가지는 의사결정나무를 얻는 경우에 빈번히 발생 • 검증용 자료(Test Data)에 의한 교차 타당성(Cross Validation) 평가나 가지치기에ㅐ 의해서 안정성 있는 의사결정나무를 얻는 것이 필요 |