Article 5. 서포트 벡터 머신 3215
Section 1. 분석기법
Paragraph 1. 서포트 벡터 머신(Support Vector Machine; SVM) 개념
- 서포트 벡터 머신은 데이터를 분리하는 초평면(Hyperplane) 중에서 데이터들과 거리가 가장 먼 초평면을 선택하여 분리하는 지도 학습 기반의 이진 선형 분류 모델이다.
- 기계학습의 한 분야로 사물 인식, 패턴 인식, 손 글씨 숫자 인식 등 다양한 분야에서 활용 되고 있는 지도 학습 모델이다.
- 최대 마진(Margin; 여유 공간)을 가지는 비확률적
선형 판별에 기초한 이진 분류기이다.
Paragraph 2. 서포트 벡터 머신 특징
- SVM은 공간상에서 최적의 분리 초평면(Hyperplane)을 찾아서 분류 및 회귀를 수행한다.
- SVM은 변수 속성 간의 의존성은 고려하지 않으며 모든 속성을 활용하는 기법이다.
- SVM은 훈련 시간이 상대적으로 느리지만, 정확성이 뛰어나며 다른 방법보다 과대 적합의 가능성이 낮은 모델이다.
Paragraph 3. 서포트 벡터 머신 종류
SVM에는 하드 마진 SVM과 소프트 마진 SVM으로 나눌 수 있다.
| 종류 | 설명 |
|---|---|
| 하드 마진 SVM (Hard Margin SVM) |
• 마진의 안쪽이나 바깥쪽에 절대로 잘못 분류된 오 분류를 허용하지 않은 SVM • 노이즈로 인하여 최적의 결정 경계를 잘못 구할 수도 있고, 못 찾을 경우도 발생할 수가 있음 |
| 소프트 마진 SVM (Soft Margin SVM) |
• 마진의 안쪽이나 바깥쪽에 절대로 잘못 분류된 오 분류를 허용하는 SVM • 하드 마진 SVM은 적용하기가 어려우므로 어느 정도의 오류를 허용하는 소프트 마진 SVM을 주로 이용 |
Paragraph 4. 서포트 벡터 머신의 구성요소
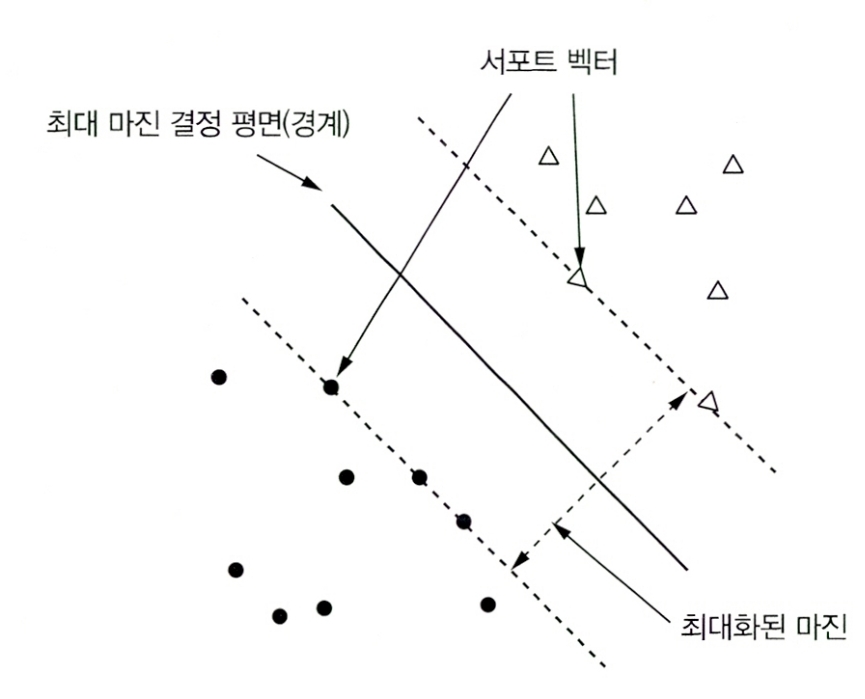
| 구성요소 | 설명 |
|---|---|
| 결정 경계 (Decision Boundary) |
• 데이터 분류의 기준이 되는 경계 |
| 초평면 (Hyperplane) |
• n 차원의 공간의 (n-1) 차원 평면 |
| 마진 (Margin) |
• 결정 경계에서 서포트 벡터까지의 거리(즉, 여유 공간) • 최적의 결정 경계는 마진을 최대화(Maximize) |
| 서포트 벡터 (Support Vector) |
• 학습 데이터 중에서 결정 경계ㅔㅔㅔ와 가장 가까이에 있는 데이터들의 집합 |
| 슬랙 변수 (Slack Variables 또는 여유변수) |
• 완벽한 분리가 불가능할 때 선형적으로 분류를 위해 허용된 오차를 위한 변수 • Soft Margin SVM에서 사용 |
Paragraph 5. 서포트 벡터 머신 적용 기준
선형으로 분리가 가능한지 불가능한지에 따라 적용하는 방식이 다르다.
| 기준 | 설명 |
|---|---|
| 선형으로 분리 가능한 SVM | • 최적의 결정 경계(또는 초평면)를 기준으로 1과 -1로 구분하여 분류 모형으로 사용 |
| 선형으로 분리 불가능한 SVM | • 저차원 공간을 고차원 공간으로 매핑할 경우에 발생하는 연산의 복잡성은 커널 트릭을 통하여 해결이 가능• 커널 트릭은 커널 함수(저차원에서 함수의 계산만으로 원하는 풀이가 가능한 함수)를 이용하여 고차원 공간으로 매핑 할 경우에 증가하는 연산량의 문제를 해결하는 기법 |
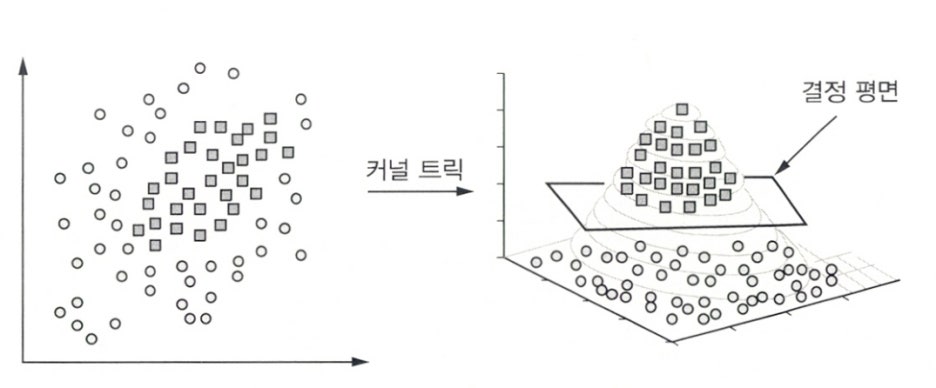
- 2차원에서 분류할 수 없는 문제를 3차원으로 매핑하여 선형 분류할 수 있다.
- 적용 가능한 대표적인 커널 함수를 다항식 커널(Polynomial Kernel), 가우시안 RBF 커널(Gaussian Radial Basis Function Kernel), 시그모이드 커널(Sigmoid Kernel) 등이 있고, 주로 가우시안 RBF 커널 함수를 많이 사용한다.
- 커널 함수의 선택에는 명확한 규칙이 없으며 실제 어떤 커널 함수를 적용하더라도 적확도에는 큰 차이가 없다.
