Article 1. 범주형 자료 분석 3221

3 minute read

범주형 자료 분석은 종속변수가 하나이고 범주형인 데이터를 분석하여 모형의 유의성과 독립변수의 유의성을 알아보는 분석 방법이다.
범주형 자료 분석은 독립변수와 종속변수의 척도에 따라 분석기법이 다르다.

⬇척도에 따른 범주형 자료 분석 방법

독립변수	종속변수	분석 방법
범주형	범주형	• 분할표 분석 • 교차 분석(카이제곱 검정) • 피셔의 정확 검정
수치형	범주형	• 로지스틱 회귀 분석

Paragraph 1. 분할표(Contingency Table)분석

분할표를 이용한 범주형 자료 분석은 상대위험도와 승산비를 통하여 분석한다.
범주형 자료의 개수에 따라 1개의 범주형 변수에 의한 1원(One-way) 분할표와 2개의 범주형 변수에 의한 2원(Two-way) 분할표, 3개 이상의 범주형 변수에 의한 다원(Multi-way) 분할표로 나눌 수 있다.
분할표의 행은 독립변수, 열은 종속변수로 배치한다.
분할표의 각 행의 마지막 행과 각 열의 마지막 열에는 총계 데이터를 표시한다. 이러한 행 또는 열을 Margin Sum(주변 합)이라고 부른다.

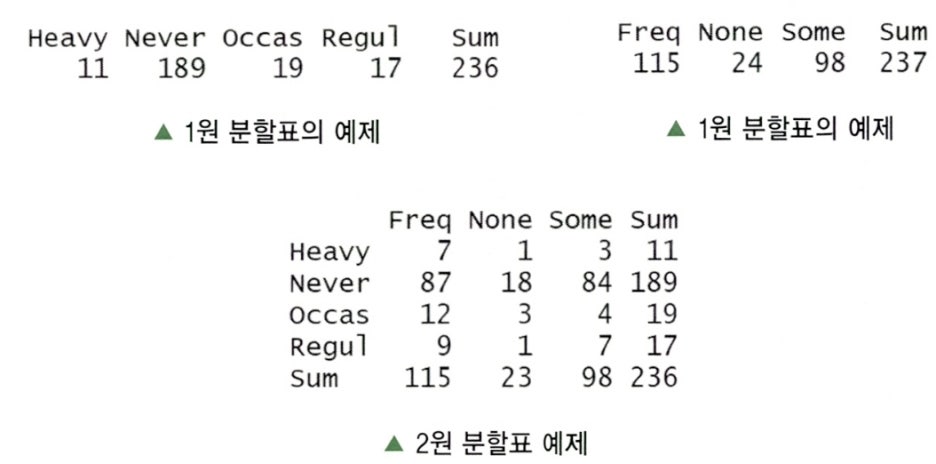
흡연 빈도에 따른 운동 빈도의 관계를 살펴보기 위한 2원 분할표 예제이다.

Subparagraph 1. 상대위험도

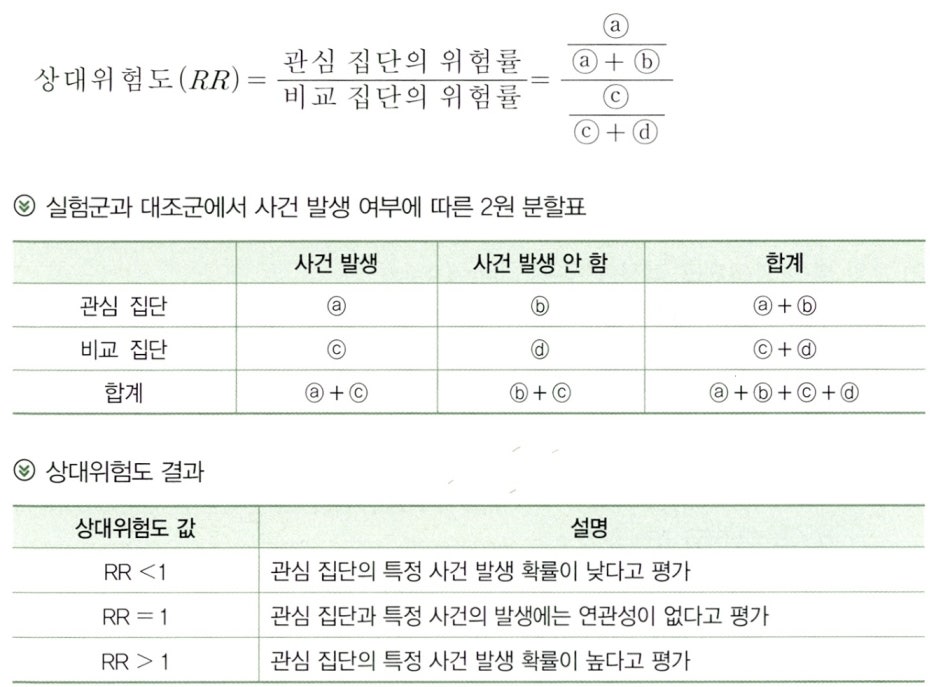
Clause 1. 상대위험도(Relative Risk; RR) 개념

상대위험도란 관심 집단의 위험률과 비교 집단의 위험률에 대한 비(Ratio)이다.
여기에서 위험률은 특정 사건(예를 들어 질병)이 발생할 비율이다.

Clause 2. 상대위험도 계산

상대위험도는 아래의 2원 분할표를 기준으로 다음과 같이 계산할 수 있다.

Subparagraph 2. 승산(Odds) 개념

승산은 특정 사건이 발생할 확률에 대한 그 사건이 발생하지 않을 확률의 비다.
특정 사건(예를 들어 우승)의 발생 확률을 p라고 하였을 경우 승산(Odds) = p / (1 - p)

예)

한국이 축구에서 브라질에 승리할 확률이 20%라고 할 때 Odds는

이길확률 / (1 - 이길확률) = 0.2 / 0.8 = 1 /4

이므로 승산은 0.25이다. (질 확률이 4배가 높다)

Subparagraph 3. 승산비(Odds Ratio; 교차비; 대응위험도) 개념

승산비는 특정 조건이 있을 때의 성공 승산을 다른 조건이 있을 때의 성공 승산으로 나눈 값이다.

Paragraph 2. 교차 분석(카이제곱 검정; Chi-Squared Test)

카이제곱 검정의 χ2 값은 편차의 제곱 값을 기대빈도로 나눈 값들의 합이다.
교차 분석은 적합도 검정(Goodness of Fit Test), 독립성 검정(Test of Independence), 동질성 검정(Test of Homogeneity)의 3가지로 분류할 수 있다.

$\chi^{2}=\sum \frac{\left({O}_{i}-E_{i}\right)^{2}}{E_{i}}$

$\chi^2$	=	chi squared
${O}_i$	=	observed value
$E_{i}$	=	expected value

Subparagraph 1. 적합도 검정

Clause 1. 적합도 검정(Goodness of Fit Test)의 개념

적합도 검정은 표본 집단의 분포가 주어진 특정 이론을 따르고 있는지를 검정하는 기법이다.
적합도 검정의 자료를 구분하는 범주가 상호 배타적이어야 한다.

예)

성별(남자, 여자), 등수
적합도 검정에서 귀무가설은 ‘표본 집단의 분포가 주어진 특정 분포를 따른다.’로 설정한다.
관찰 빈도와 기대빈도의 차이가 클수록 귀무가설을 기각할 확률이 높아진다.

적합도 검정 자유도

자유도 = 범주의 수 - 1

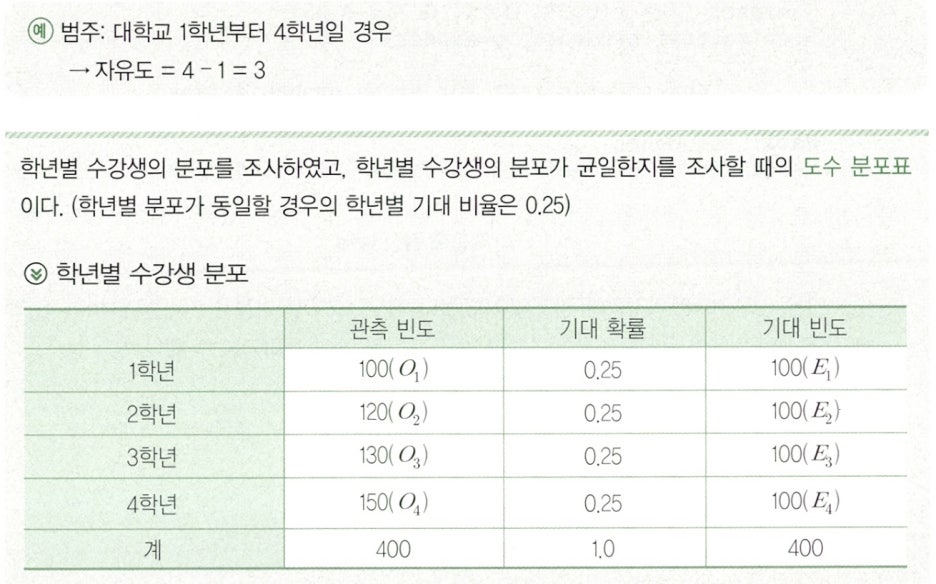
Clause 2. 적합도 검정 방법

Subparagraph 2. 독립성 검정

Clause 1. 독립성 검정(Test of Independence)의 개념

독립성 검정은 여러 범주를 가지는 2개의 요인이 독립적인지, 서로 연관성이 있는지를 검정하는 기법이다.

예)

학년(1학년, 2학년, 3학년)이라는 범주형 데이터(요인 1)와 선호과목(국, 영, 수)이라는 범주형 데이터(요인 2) 간에 서로 연관성이 있는 것인지 아니면 독립적인지를 판단하는 것과 같은 문제에 독립성 검정을 사용한다.
독립성 검정에서의 귀무가설은 ‘요인 1과 요인 2는 독립적이다’로 설정한다

독립성 검정 자유도

자유도 = { ( 범주 1의 수) - 1} × { ( 범주 2의 수 ) - 1}

예)

범주 1이 대학교 1학년부터 4학년이고 범주 2가 학점(A, B, C, D, F)일 경우

자유도는 (4 - 1) × (5 - 1) = 12

Clause 2. 독립성 검정 방법

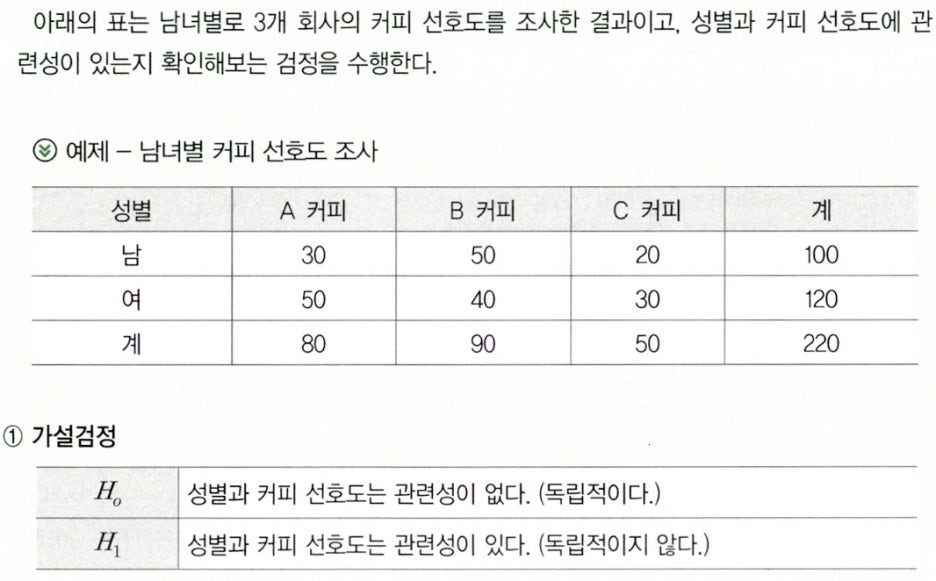
Subparagraph 3. 동질성 검정

Clause 1. 동질성 검정(Test of Homogeneity)의 개념

동질성 검정은 각각의 독립적인 부모집단으로부터 정해진 표본의 크기만큼 자료를 추출하는 경우에 관측값들이 정해진 범주 내에서 서로 동질한지(비슷하게 나타나고 있는지) 여부를 검정하는 기법이다.

예)

남학생과 여학생 그룹에 대하여 각 그룹이 선호하는 과목이 같은지 여부를 판단하는 것과 같은 문제에 동질성 검정을 사용

Clause 2. 동질성 검정 특징

독립성 검정은 두 변수가 서로 독립인지 아닌지에 대한 판단이고 동질성 검정은 각 부모집단의 동질성 여부를 검정하는 차이가 있다.
동질성 검정에서의 귀무가설은 ‘모집단은 동질하다’로 설정한다.

예)

남학생과 여학생이 선호하는 과목은 동일

동질성 검정과 검정은 개념상의 차이만 있을 뿐 계산 방식은 동일하다.

Paragraph 3. 피셔의 정확 검정(Fisher’s Exact Exam)

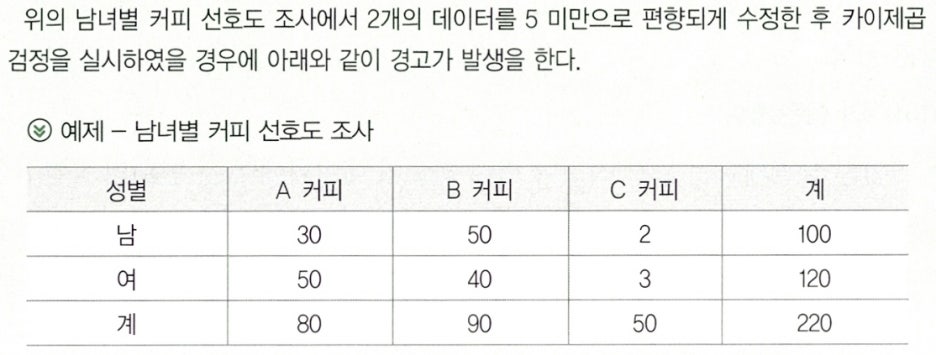
분할표에서 표본 수가 적거나 표본이 셀에 치우치게 분포되어 있을 경우 피셔의 정확 검정을 실시한다.
범주형 데이터에서 기대빈도가 5 미만인 셀이 20%를 넘는 경우 카이제곱 검정의 정확도가 떨어지므로 피셔 정확 검정을 사용한다.

Twitter Facebook LinkedIn

goaswon