Article 2. 다변량 분석 3222

Section 2. 고급 분석기법

Paragraph 1. 상관 분석

Subparagraph 1. 피어슨 상관계수

• 피어슨 상관계수는 등간 척도나 비례 척도의 데이터에서 두 변수의 공분산을 표준편차의 곱으로 나눈 값이다
• 두 변수 간 선형관계의 크기를 측정하는 값으로 비선형적인 상관관계는 나타내지 못한다.
• 피어슨 상관계수는 모집단, 표본에 적용할 수 있다.

Subparagraph 2. 스피어만의 상관계수(Spearman’s Rank Correlation Coefficient)

• 스피어만 상관계수는 두 변수 간의 비선형적인 관계도 나타낼 수 있는 값이다.
• 두 변수를 모두 순위로 변환시킨 후 두 순위 사이의 스피어만 상관계수를 구한다.

Paragraph 2. 다차원 척도법

Subparagraph 1. 다차원 척도법(MultiDimensional Scaling; MDS) 개념

개체들 사이의 유사성, 비유사성을 측정하여 2차원 또는 3차원 공간상에 점으로 표현하여 개체들 사이의 집단화를 시각적으로 표현하는 분석 방법이다.

Subparagraph 2. 다차원 척도법 방법

• 개체들의 거리는 유클리드 거리행렬을 이용한다.
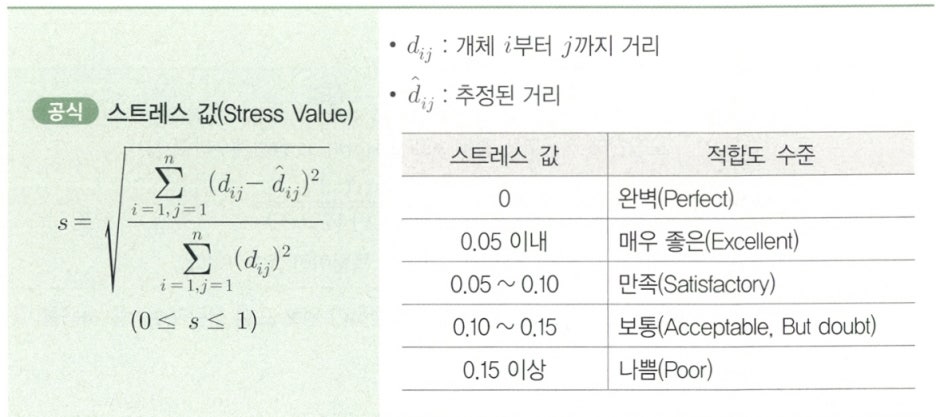
• 다차원 척도법에서는 스트레스 값(Stress Value)을 이용하여 관측 대상들의 적합도 수준을 나타낸다.
• 스트레스 값은 0에 가까울수록 적합도 수준이 완벽하고 1에 가까울수록 나쁘다.

Subparagraph 3. 다차원 척도법 종류

종류	내용
계량적 다차원 척도법	• 데이터가 연속형 변수인 경우로 구간 척도나 비율 척도에 사용함 • 유클리드 거리 행렬을 이용하여 개체들 간의 실제거리를 계산하고 개체들간의 비유사성을 공간상에 표현한다.
비 계량적 다차원 척도법	• 데이터가 순서 척도인 경우에 사용함 • 개체들 간 거리가 순서로 주어진 경우에는 개체들 간 절대적 거리는 무시하고 순서척도를 거리의 속성과 같도록 변환하여 거리를 생성함

Paragraph 3. 주성분 분석

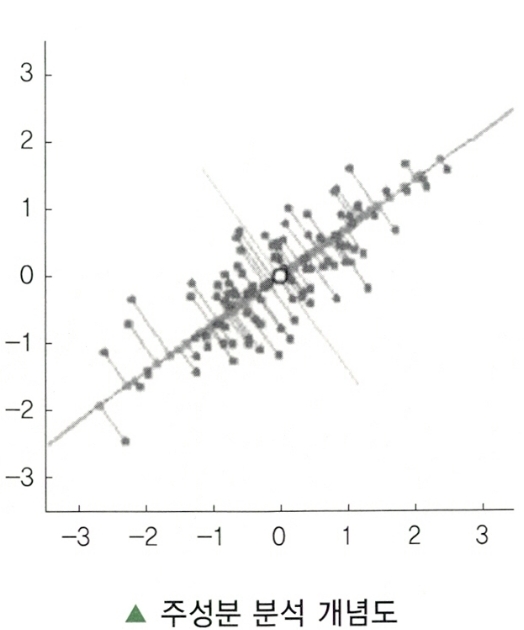
Subparagraph 1. 주성분 분석(Principal Component Analysis: PCA)의 개념

• 상관관계가 있는 고차원 자료를 자료의 변동을 최대한 보존하는 저차원 자료로 변환하는 차원축소 방법이다.
• 주성분 분석은 서로 상관성이 높은 변수들의 선형 결합으로 만들어 기존의 상관성이 높은 변수들을 요약, 축소하는 기법이다.
• 분석을 통해 나타나는 주성분으로 변수들 사이의 구조를 쉽게 이해하기는 어렵다.
• 차원 축소는 고윳값이 높은 순으로 정렬해서, 높은 고윳값을 가진 고유벡터만으로 데이터를 복원한다.

Subparagraph 2. 주성분 분석의 특징

• 자료의 차원을 축약시키는 데 주로 사용된다.
• p 차원 변수 X = (X₁, X₂, ⋅⋅⋅, Xₚ)ᵀ
• p개의 변수들을 중요한 m(P) 개의 주성분으로 표현하여 전체 변동을 설명하는 것으로 m개의 주성분은 원래 변수들의 선형 결합으로 표현된다.
• 누적 기여율이 85% 이상이면 주성분의 수로 결정할 수 있다.
• 차원 감소폭의 결정은 스크린 산점도(Scree Plot), 전체 변이의 공헌도, 평균 고윳값 등을 활용하는 방법이 있다.
• 주성분 분석에서 차원의 저주는 데이터 차원이 증가할 때, 데이터의 구조를 변환하여 불필요한 정보도 최대한 축적하는 차원 감소 방법으로 해결이 필요하다.