Article 4. 베이지안 기법 3224

Section 2. 고급 분석기법

Paragraph 1. 확률 및 기본 통계 이론

Subparagraph 1. 확률(Probability)의 개념

• 비슷한 현상이 반복해서 일어날 경우에 어떤 사건이 발생할 가능성을 숫자로 표현하는 방법이다.
• 같은 원인에서 특정한 결과가 나타나는 비율이라고도 한다.

Subparagraph 2. 확률의 계산

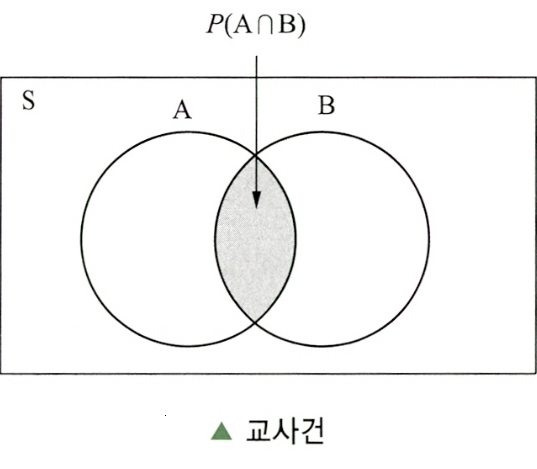
Subparagraph 3. 교사건(Intersection of Events)

사건 A와 B에 동시에 속하는 기본 결과들의 모임 (A∩B)이다.

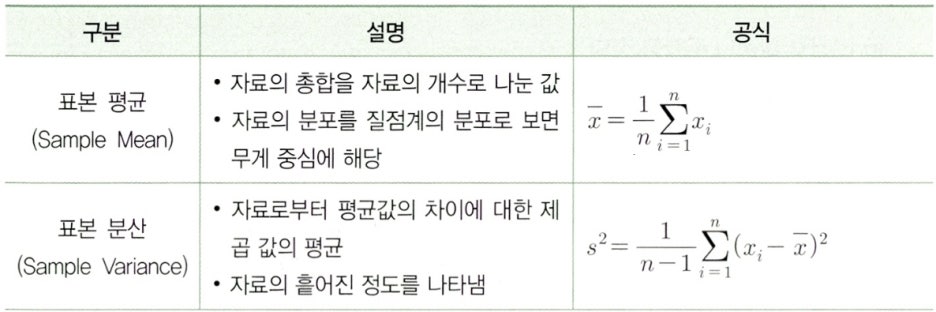
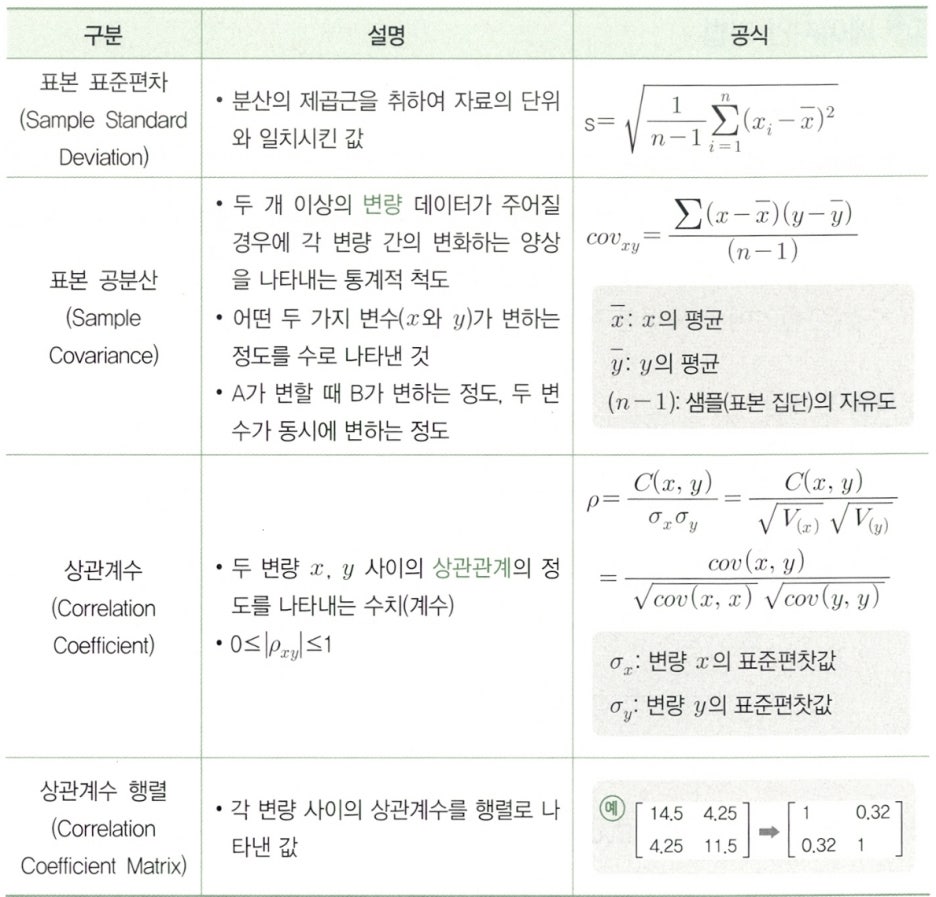
Subparagraph 4. 통계 파라미터

Paragraph 2. 조건부 확률

Subparagraph 1. 조건부 확률(Conditional Probability)의 개념

• 어떤 사건이 일어난다는 조건에서 다른 사건이 일어날 확률이다.
• 두 개의 사건 A와 B에 대해서 사건 A가 일어난다는 선행조건 아래에 사건 B가 일어날 확률이다.

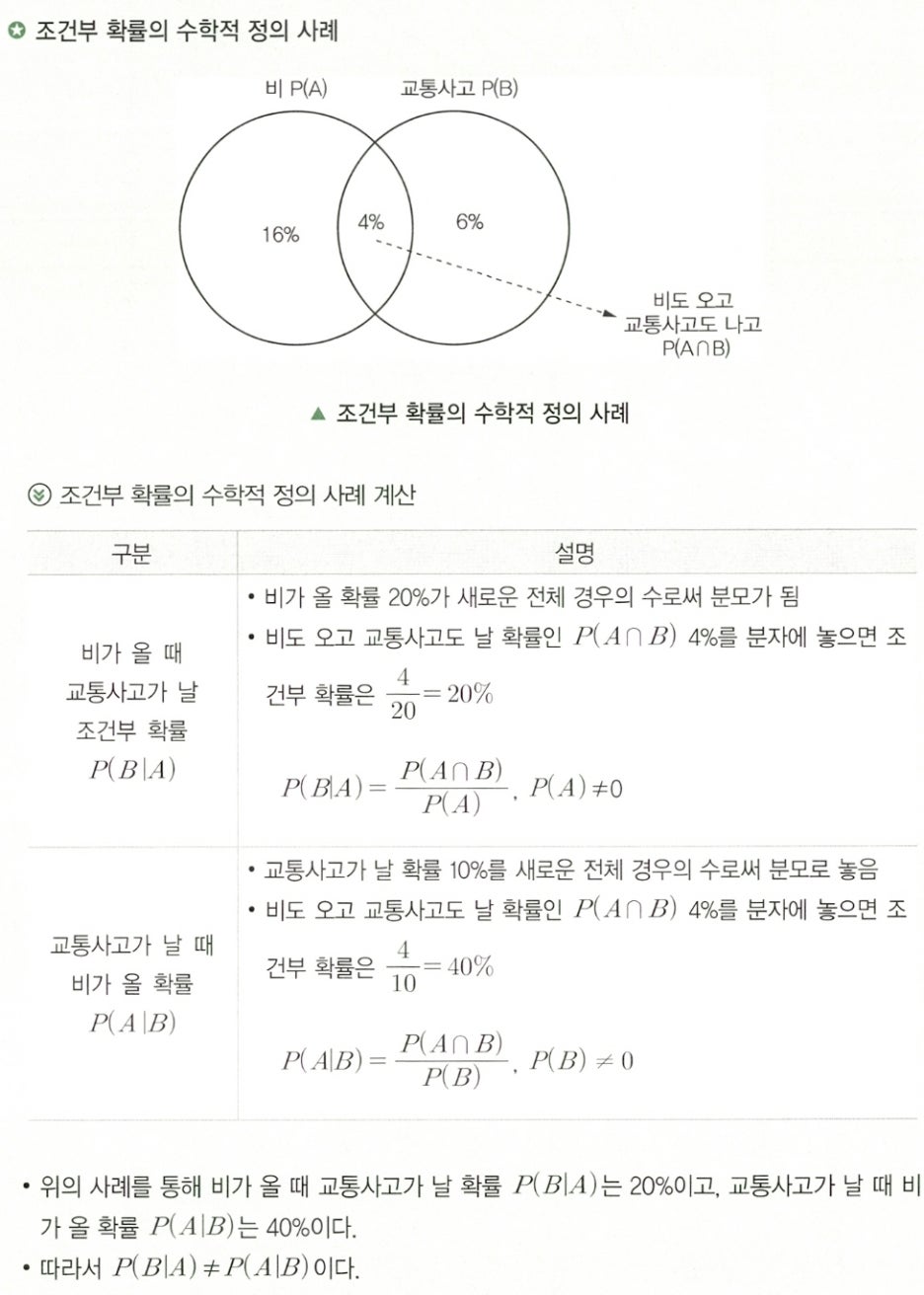
Subparagraph 2. 조건부 확률의 수학적 정의

Paragraph 3. 전 확률의 정리

Subparagraph 1. 전 확률의 정리(Law of Total Probability) 개념

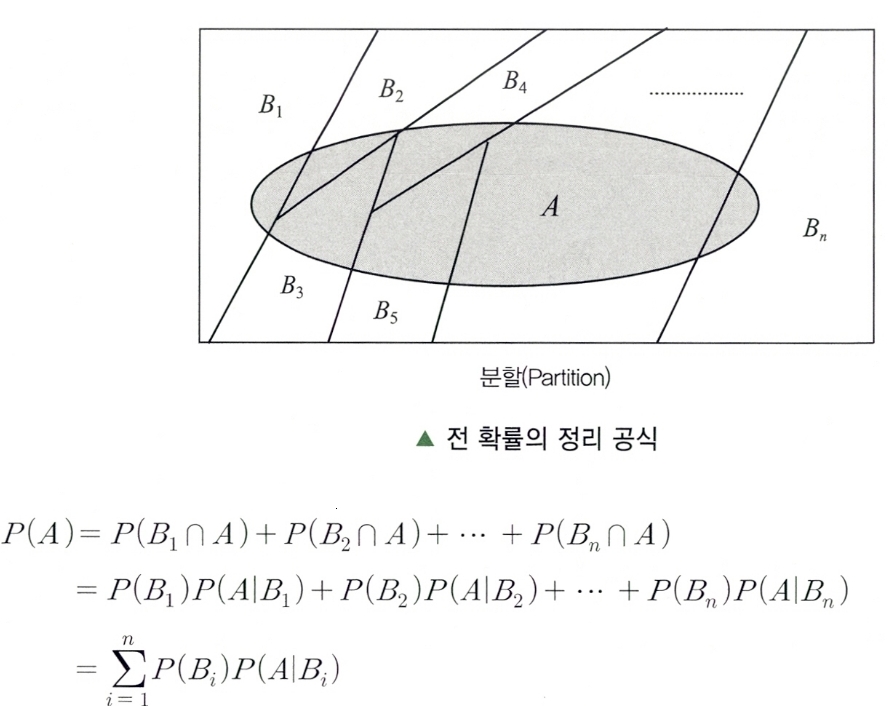
• 나중에 주어지는 사건 A의 확률을 구할 때, 그 사건의 원인을 여러 가지로 나누어서, 각 원인에 대한 조건부 확률 *P(A

  Bᵢ)*의 곱에 의한 가중합(Σ)으로 구할 수 있다는 법칙이다.

Subparagrpah 2. 전 확률의 정리 공식

Paragraph 4. 베이즈 정리

Subparagraph 1. 베이즈 정리(Bayes’ Theorem) 개념

• 베이즈 정리는 어떤 사건에 대해 관측 전(사전 확률) 원인에 대한 가능성과 관측후(사후 확률)의 원인 가능성 사이의 관계를 설명하는 확률이론이다.
• 어떤 사건 B가 서로 배반인 A₁, A₂, A₃, ⋅⋅⋅, Aₙ 중 어느 한 가지 경우로 발생하는 경우 실제 B가 일어날 때, 이것이 Aᵢ일 확률을 베이즈 확률이라고 한다.

Subparagraph 2. 베이즈 정리의 표현 식의 이해

• *P(Aᵢ

  B)*의 직관적인 표현식은 다음과 같이 표현할 수 있다.

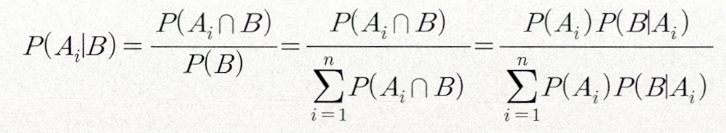
• 위 식은 B를 표본공간 S내 임의의 사상이라고 하고, 서로 배반이 사상 A₁, A₂, A₃, ⋅⋅⋅, Aₙ의 합(Union) 사상이 표본공간 S라 하면, B 사건을 근거로 Aᵢ 사건이 발생할 확률을 의미한다.

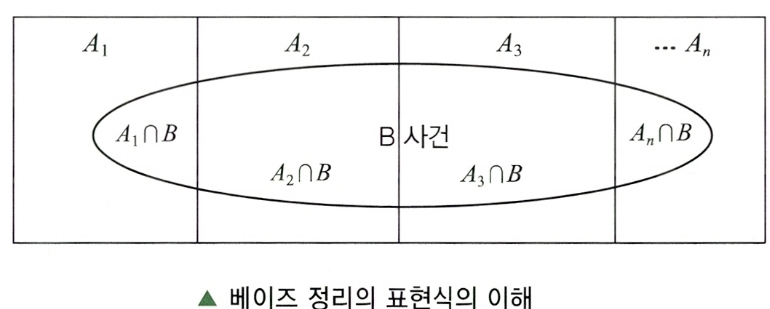
• 조건부 확률에서 정의한 식 변환에 의해 아래와 같이 표현할 수 있다.