Article7. 앙상블 분석 3227
Section 2. 고급 분석기법
Paragraph 1. 앙상블(Ensemble) 개념
- 여러 가지 동일한 종류 또는 서로 상이한 모형들의 예측/분류 결과를 종합하여 최종적인 의사결정에 활용하는 기법이다.
- 앙상블이란 본래 프랑스어로 ‘통일, 조화’ 등을 나타내는 용어이다.
Paragraph 2. 앙상블의 특징
| 특징 | 설명 |
|---|---|
| 보다 높은 신뢰성 확보 | 다양한 모형의 예측 결과를 결ㄹ합함으로써 단일 모형으로 분석했을 때보다 높은 신뢰성 |
| 정확도(Accuracy) 상승 | 이상값에 대한 대응력이 높아지고, 전체 분산을 감소시킴 |
| 원인분석에 부적합 | 모형의 투명성이 떨어지게 되어 정확한 현상의 원인분석에는 부적합 |
Paragraph 3. 앙상블 알고리즘
- 주어진 자료로부터 여러 개의 예측 모형을 만든 후 예측 모형들을 조합하여 하나의 최종 예측 모형을 만드는 방법으로 다중 모델 조합(Conbining Multiple Models), 분류기 조합(Classifier Combination)이 있다.
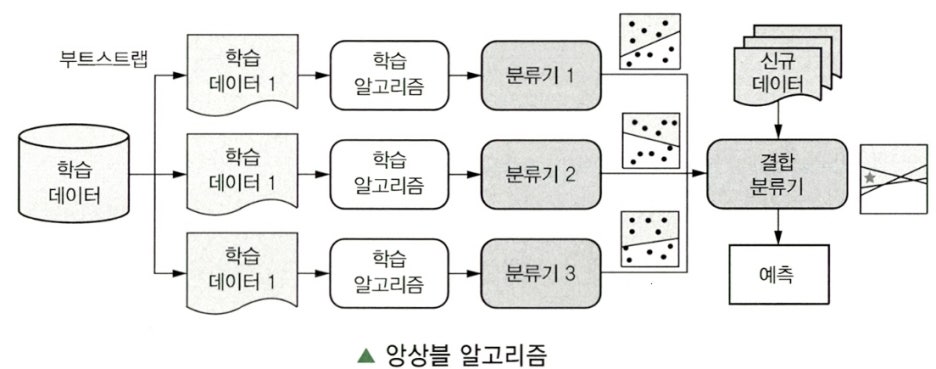
- 앙상블 알고리즘은 여러 개의 학습 모델을 훈련하고 투표를 통해 최적화된 예측을 수행하고 결정한다.
- 학습 데이터의 작은 변화에 의해 예측 모형이 크게 변하는 경우, 그 학습 방법은 불안정하다.
- 가장 안정적인 방법으로는 1-nearest neighbor(가장 가까운 자료만 변하지 않으면 예측 모형이 변하지 않음), 선형 회귀 모형(
최소제곱법으로 추정해 모형 결정)이 존재한다.
Paragraph 4. 앙상블 학습절차
앙상블 학습절차는 도출 및 생성, 집합별 모델 학습, 결과 조합, 최적 의견 도출로 진행된다.
| 순서 | 학습절차 | 설명 |
|---|---|---|
| 1 | 도출 및 생성 | 학습 데이터에서 여러 학습 집합들을 도출 |
| 2 | 집합별 모델 학습 | 각 집합으로부터 모델을 학습 |
| 3 | 결과 조합 | 각 학습 모델로부터의 결과를 조합 |
| 4 | 최적 의견 도출 | 학습된 모델들의 최적 의견을 도출 |
Paragraph 5. 앙상블 기법의 종류
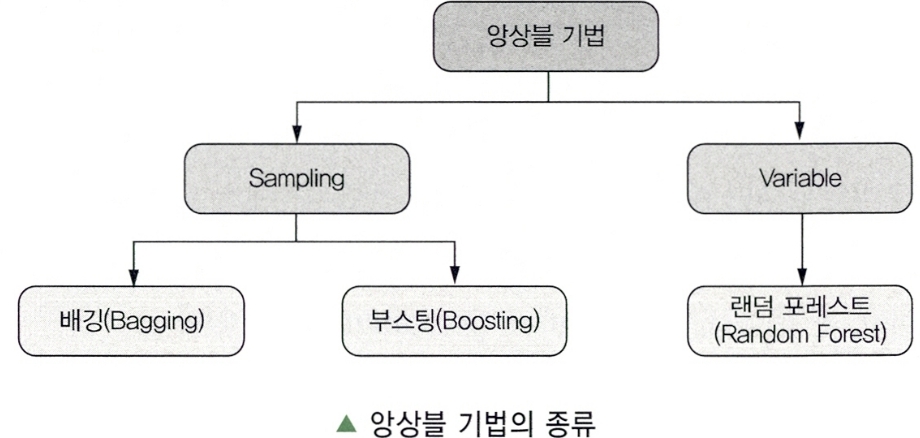
Subparagraph 1. 배깅
Clause 1. 배깅(Bagging; Bootstrap Aggregating)의 개념
- 배깅은 학습 데이터에서 다수의 부트스트랩(Bootstrap) 자료를 생성하고, 각 자료를 모델링한 후 결합하여 최종 예측 모형을 만드는 알고리즘이다.
부트스트랩은 주어진 자료에서 동일한 크기의 표본을 랜덤복원추출로 뽑은 자료를 의미한다.
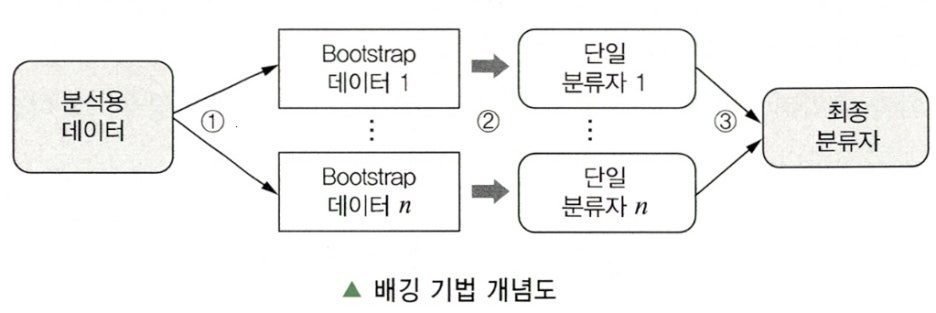
Clause 2. 배깅 기법 절차
| 순서 | 절차 | 설명 |
|---|---|---|
| 1 | 부트스트랩 데이터 추출 | 분석용 데이터로부터 n개의 부트스트랩 데이터 추출(동일 크기) |
| 2 | 단일 분류자 생성 | 부트스트랩 데이터에 적합한 모델을 적용하여 n개 단일 분류자 생성 |
| 3 | 최종 모델 결정 | n개의 단일 분류자 중 다수결(Majority Voting)을 통해 최종 모델 결정 |
보팅은 여러 개의 모형으로부터 산출된 결과를 다수결에 의해서 최종 결과를 선정하는 과정이다.- 최적의 의사결정나무를 구축할 때 가장 어려운 부분이 가지치기(Pruning)이지만 배깅에서는 가지치기를 하지 않고 최대한 성장한 의사결정나무들을 활용한다.
- 실제 현실에서는 학습 자료의 모집단 분포를 모르기 때문에 평균 예측 모형을 구할 수 없기 때문에 배깅은 이러한 문제를 해결하기 위해 훈련자료를 모집단으로 생각하고 평균 예측 모형을 구하여 분산을 줄이고 예측력을 향상시킬 수 있다.
Clause 3. 배깅 기법 특징
-
목표
- 전반적으로 분류를 잘할 수 있도록 유도(분산감소)
-
최적 모델 결정 방법
- 독립수행 후 다수결로 결정
- 연속형 변수와 범주형 변수에 따라 방법이 다름
- 연속형 변수
- 다중 투표(Majority Voting)
- 범주형 변수
- 평균(Average)
-
장점
- 일반적으로 성능 향상에 효과적
- 결측값이 존재할 때 강함
-
단점
- 계산 복잡도는 다소 높음
-
적용 방안
- 소량 데이터(데이터 세트의 관측값의 수)일수록 유리
- 목표변수, 입력변수의 크기가 작아 단순할수록 유리
-
주요 알고리즘
- MetaCost Algorithm
Subparagraph 2. 부스팅
Clause 1. 부스팅(Boosting)의 개념
- 잘못 분류된 개체들에 가중치를 적용, 새로운 분류 규칙을 만들고, 이과정을 반복해 최종 모형을 만드는 알고리즘이다.
- 예측력이 약한 모형(Weak Learner)들을 결합하여 강한 예측 모형을 만드는 방법이다.
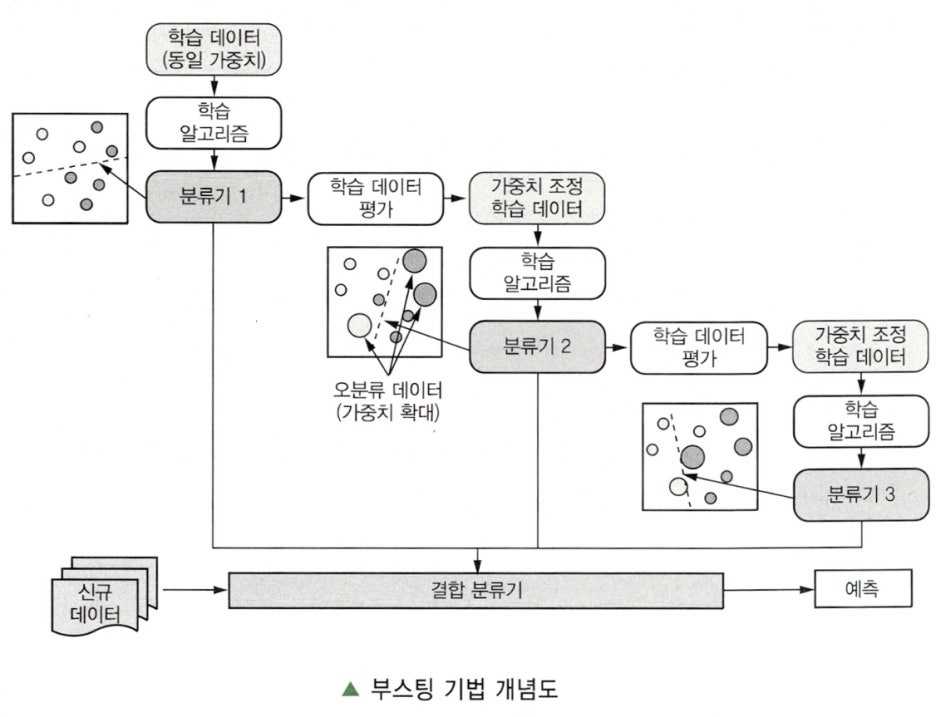
Clause 2. 부스팅 기법 절차
| 순서 | 절차 | 설명 |
|---|---|---|
| 1 | 동일 가중치 분류기 생성 | 동일한 가중치의 분석용 데이터로부터 분류기 생성 |
| 2 | 가중치 변경 통한 분류기 생성 | 이전 분석용 데이터의 분류 결과에 따라 가중치 변경을 통해 분류기 생성 |
| 3 | 최종 분류기 결정 | 목표하는 정확성이 나올 때까지 N회 반복 후 최종 분류기 결정 |
Clause 3. 부스팅 기법 특징
| 구분 | 설명 |
|---|---|
| 목표 | • 분류하기 힘든 관측값들에 대해서 정확하게 분류를 잘하도록 유도(예측력 강화) |
| 최적 모델 결정 방법 |
• 순차 수행에 따른 가중치 재조정으로 결정 • 이전 분류에서 정 분류 데이터에는 낮은 가중치 부여 • 이전 분류에서 오 분류 데이터에는 높은 가중치 부여 |
| 특장점 | • 특정 케이스의 경우 상당히 높은 성능을 보임 • 일반적으로 과대 적합(Over-fitting) 없음 |
| 계산 복잡도 | • 다소 높은 계산 복잡도 |
| 적용 방안 | • 대용량 데이터일수록 유리 • 데이터와 데이터의 속성이 복잡할수록 유리 |
| 주요 알고리즘 | • AdaBoost(Adaptive Boost) Algorithm |
- 부스팅 방법 중 Freund&Schapire가 제안한 AdaBoost는 이진 분류 문제에서 랜덤 분류기보다 조금 더 좋은 분류기 n개에 각각 가중치를 설정하고 n개의 분류기를 결합하여 최종 분류기를 만드는 방법을 제안했다. (단, 가중치의 합은 1)
- 배깅에 비해 많은 경우 예측 오차가 향상되어 AdaBoost의 성능이 배깅보다 뛰어난 경우가 많다.
Subparagraph 3. 랜덤 포레스트
Clause 1. 랜덤 포레스트(Random Forest)의 개념
- 랜덤 포레스트는 의사결정나무의 특징인 분산이 크다는 점을 고려하여 배깅과 부스팅보다 더 많은
무작위성을 주어 약한 학습기들을 생성한 후 이를 선형 결합하여 최종 학습기를 만드는 방법이다.
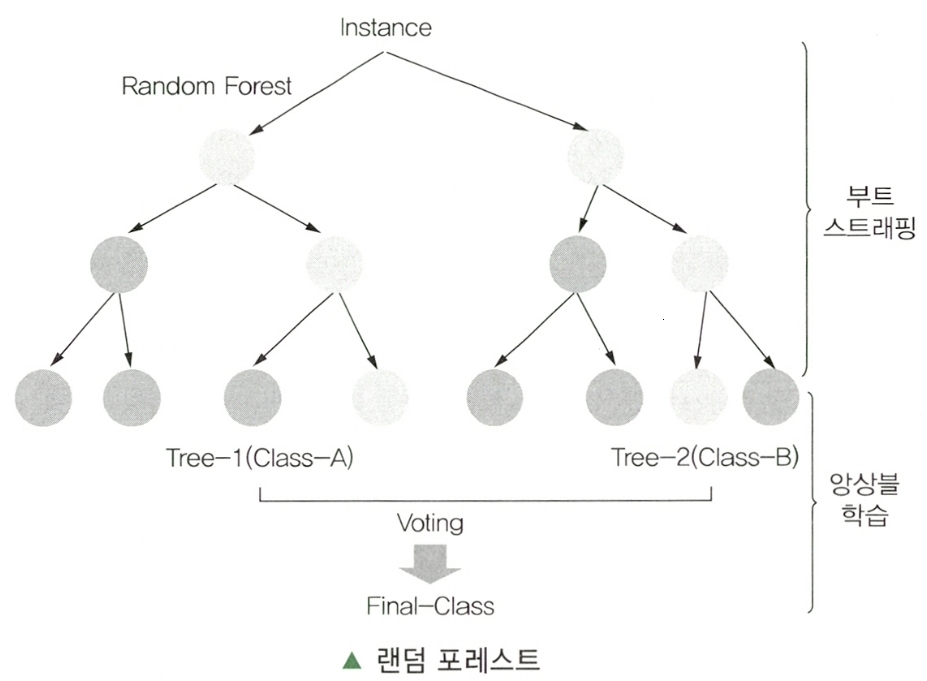
- 랜덤 포레스트 패키지는 랜덤 입력(Random Input)에 따른 여러 트리(Tree)의 집합인 포레스트(Forest)를 이용한 분류 방법이다.
Clause 2. 랜덤 포레스트 절차
| 순서 | 절차 | 설명 |
|---|---|---|
| 1 | 데이터 추출 | 분석용 데이터로부터 N개의 부트스트랩 데이터 추출 |
| 2 | 대표 변수 샘플 도출 | N개의 분류기를 훈련 후 대표 변수 샘플 도출 |
| 3 | Leaf Node로 분류 | 대표 변수 샘플들을 의사결정나무의 Leaf Node로 분류 |
| 4 | 최종 모델 결정 | Leaf Node들의 선형 결합으로 최종 모델 결정 |
- 수천 개의 변수를 통해 변수 제거 없이 실행되므로 정확도 측명에서 좋은 성과를 보인다.
- 이론적 설명이나 최종 결과에 대한 해석이 어렵다는 단점이 있지만, 예측력이 매우 높다.
- 입력변수가 많은 경우, 배깅과 부스팅과 비슷하거나 좋은 예측력을 보인다.
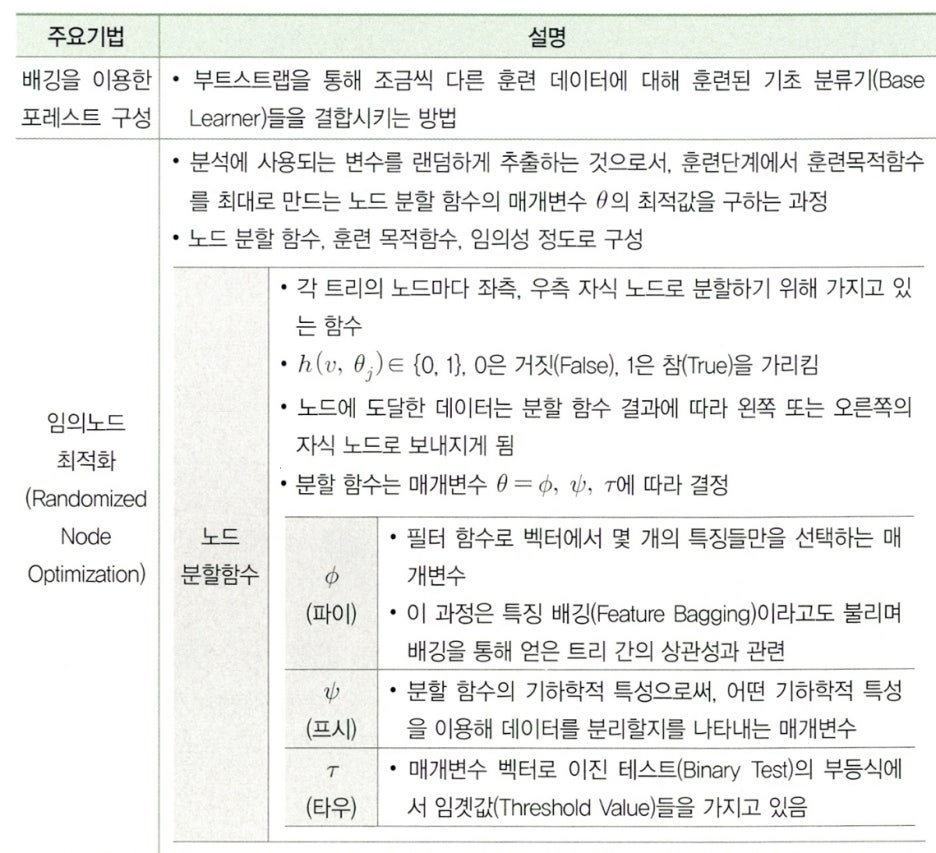
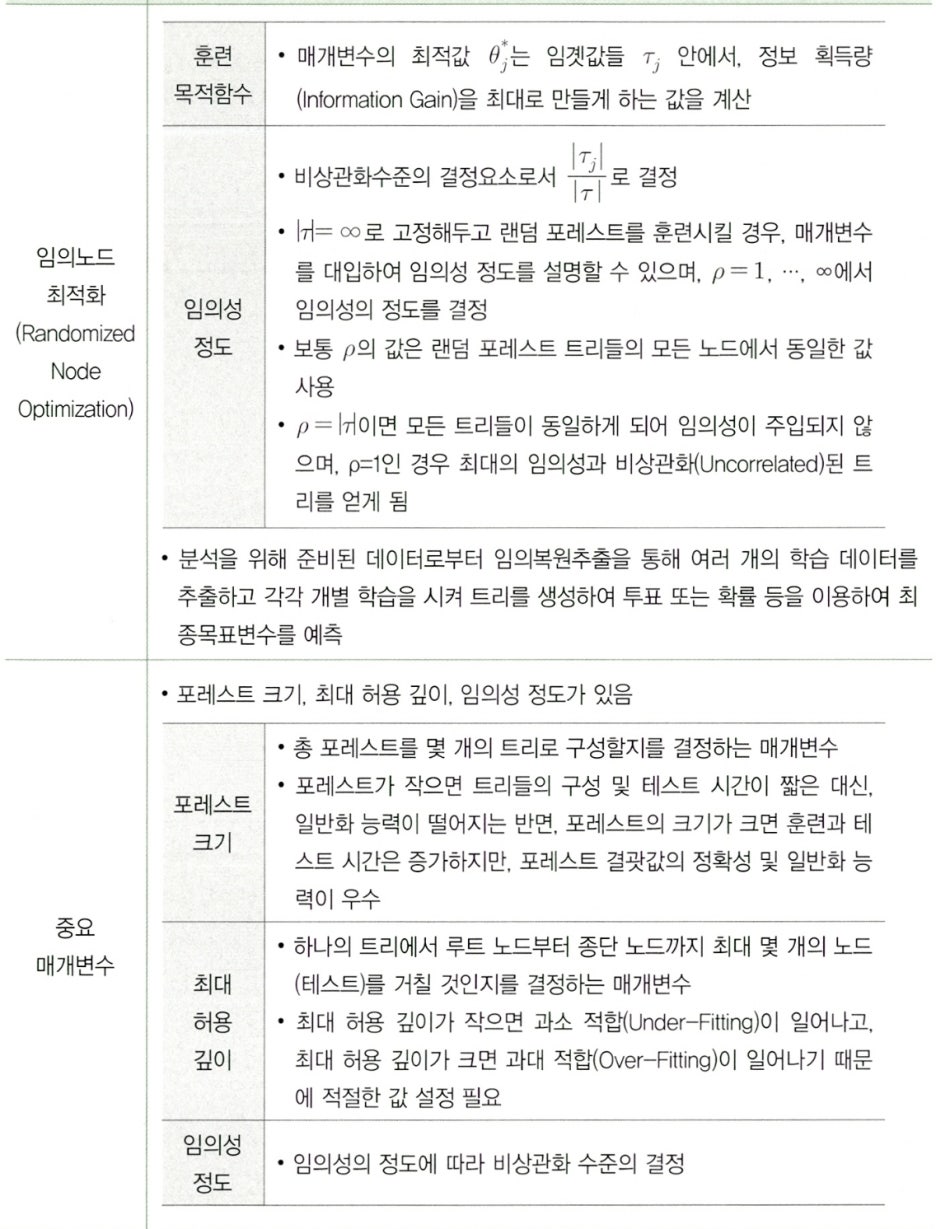
Clause 3. 랜덤 포레스트 주요기법