Article8. 비모수 통계 3228

Section 2. 고급 분석기법

Paragraph 1. 비모수 통계의 개념

• 비모수 통계는 평균이나 분산 같은 모집단의 분포에 대한 모수성을 가정하지 않고 분석하는 통계적 방법이다.
• 데이터가 모수적 분석 방법이 가정한 특성을 만족하지 못할 때는 비모수 통계분석 방법을 사용하여야 한다.

Paragraph 2. 비모수 통계 특징

• 비모수 통계분석에서는 빈도(Frequency), 부호(Sign), 순위(Rank) 등의 통계량을 사용한다.
• 순위와 부호에 기초한 방법 위주로 이상값으로 인한 영향이 적다.
• 데이터가 모수적 분석 방법이 가정한 특성을 만족하지 못할 때는 비모수 통계분석 방법을 사용하여야 한다.

Paragraph 3. 비모수 통계의 장단점

장점	단점
• 모집단의 분포에 대한 가정의 불만족으로 인한 오류의 가능성이 작다. • 모수적 방법에 비해 통계량의 계산이 간편하고 직관적으로 이해하기 쉽다. • 모집단의 분포에 무관하게 사용할 수 있다. • 추출된 샘플의 개수가 10개 미만으로 작을 경우에도 사용할 수 있다. • 이상값으로 인한 영향이 적다.	• 모수 통계로 검정이 가능한 데이터를 비모수 통계를 이용하면 효율성이 떨어진다 • 표본의 크기가 커질수록 간편하지만 지루한 반복 계산을 요구한다.

Paragraph 4. 비모수 통계 검정 방법의 종류

구분	비모수 통계	모수 통계
단일 표본	• 부호 검정(Sign Test) • 윌콕슨 부호 순위 검정(Wilcoxon Signed Rank Test)	단일 표본 T-검정
두 표본	• 윌콕슨 순위 합 테스트(Wilcoxon Rank Sum Test)	독립 표본 T-검정
두 표본	• 부호 검정(Sign Test) • 윌콕슨 부호 순위 검정(Wilcoxon Signed Rank Test)	대응 표본 T-검정
분산 분석	• 크루스칼-왈리스 검정(Kruscal-Wallis Test)	ANOVA
무작위성	• 런 검정(Run Test)	없음
상관 분석	• 스피어만 순위 상관계수(Spearman’s Rank Correlation Coefficient)	피어슨 상관계수 (Pearson’s Correlation Coefficient)

Paragraph 5. 비모수 통계 검정 방법

Subparagraph 1. 단일 표본 부호검정

Clause 1. 부호 검정(Sign Test) 개념

• 차이의 크기는 무시하고 차이의 부호만을 이용한, 중위수의 위치에 대한 검정 방법이다.
• 자료를 중위수와 차이의 부호인 +와 -의 부호로 전환한 다음 부호들의 수를 근거로 검정한다.
• 자료의 분포가 연속적이고 독립적인 분포에서 나온 것이라는 가정만 필요하다.

Clause 2. 부호 검정 절차

θ는 중위수이고 θ₀는 가정된 중위수이며 자료의 분포가 대칭이라고 가정(대칭성 가정은 반드시 필요하지 않음)한다.

Subparagraph 2. 단일 표본 부호 순위 검정

Clause 1. 윌콕슨 부호 순위 검정(Wilcoxon Signed Rank Test) 개념

• 윌콕슨 부호 순위 검정은 단일 표본에서 중위수에 대한 검정에 사용되며, 또한 대응되는(Paired) 두 표본의 중위수의 차이 검정에도 사용된다.
• 차이의 부호뿐만 아니라 차이의 상대적인 크기도 고려한 검정 방법이다.
• 자료의 분포가 연속적이고 독립적인 분포에서 나온 것이라는 기본 가정 외에 자료의 분포에 대한 대칭성 가정이 필요하다.

Clause 2. 윌콕슨 부호 순위 검정 절차

θ는 중위수이고 θ₀는 가정된 중위수이며, 자료의 분포가 대칭이라고 가정(대칭성 가정이 반드시 필요)한다.

Clause 3. 윌콕슨 부호 순위 검정의 유의 사항

• 위치 모수인 θ₀와 같은 데이터는 검정하기 전에 표본에서 제외시킨다.

• 관측값이 동점 또는 *

  Yᵢ

  *가 동점(tie)인 경우 Rᵢ⁺를 구하기 위하여 평균 순위를 사용한다. (예를 들어 순위가 2 2로 같을 경우 2와 3의 평균 순위 2.5를 사용한다.)

• 분산에도 영향을 미치므로 분산도 수정이 필요하다.

Subparagraph 3. 두 표본 검정-윌콕슨 순위 합 검정

Clause 1. 윌콕슨 순위 합 검정(Wilcoxon Rank Sum Test) 개념

• 두 표본 중위수 검정의 대표적인 비모수 검정 방법으로서 만-휘트니의 U 검정(Mann-Whitney U Statistics)과 동일하다.
• 세 사람의 이름을 모두 붙여서 만-휘트니-윌콕슨 순위 합 검정이라고ㅗ도 부른다.
• 두 표본의 혼합 표본에서 순위 합을 이용한 검정 방법이다.
• 자료의 분포가 연속적이고 독립적인 분포에서 나온 것이라는 기본 가정 외에 자료의 분포에 대한 대칭성 가정이 필요하다.

θ는 중위수이고 대칭성 가정

Clause 2. 윌콕슨 순위 합 검정 절차

• 연속적이고 동일한 분포를 가지는 분포를 가지는 두 개의 독립적인 모집단 1과 2로부터 아래와 같이 표본을 각각 추출하였다고 가정한다.

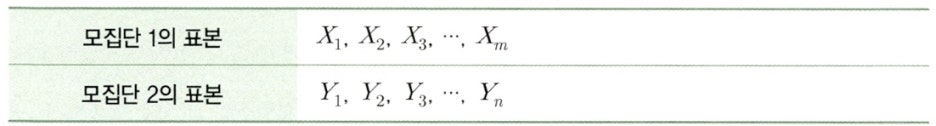
• 표본의 개수가 m ≥ n, N = m + n이고 두 모집단은 동일한 분포를 가졌다고 가정한다.
• 두 모집단 중위수의 차를 𝛥라고 하였을 때 검정 절차는 다음과 같다

Clause 3. 동점의 처리

혼합 표본에서 동점이 있을 경우 W는 동점 간의 평균 순위를 사용한다.

예)

혼합 샘플의 동점의 순위가 3과 4일 경우 평균 순위를 3.5를 사용

Subparagraph 4. 대응 표본 검정(Paired Sample Test)

• 하나의 모집단에서 두 가지 처리를 적용하여 관찰 값을 얻은 후 각 쌍의 차이를 이용하여 두 중위수 차이를 검정하는 방법이다.

예)

다이어트 약과 위약의 처방(2가지 처리)

• 대응 표본 검정에는 부호 검정과 윌콕슨 부호 순위 검정 방법을 이용한다.
• 분포가 연속이고 중위수가 θ와 θ+ẟ인 두 모집단으로부터 각 n개를 쌍으로 추출한 대응 표본을 (X₁, Y₁), (X₂, Y₂), (X₃, Y₃), ⋅⋅⋅,(Xₙ, Yₙ)이라고 할 경우 Dᵢ= Yᵢ - Xᵢ이고 i = 1, 2, 3, ⋅⋅⋅,n이라고 하며, D₁, D₂, D₃, ⋅⋅⋅,Dₙ는 연속 분포이고 중위수가 ẟ인 1개의 모집으로 추출한 n개의 표본이라고 간주할 수 있다.
• 따라서 단일 표본에서의 부호 검정과 윌콕슨 부호 순위 검정을 대응 표본 검정 방법으로 사용할 수 있다.

Subparagraph 5. 분산 분석 - 크루스칼 왈리스 검정

Clause 1. 크루스칼 왈리스 검정(Kruscal-Wallis Test) 개념

• 세 집단 이상의 분포를 비교하는 검정 방법으로 모수적 방법에서의 one-way ANOVA와 같은 목적으로 쓰인다.
• 그룹별 평균이 아닌 중위수가 같은지를 검정한다.

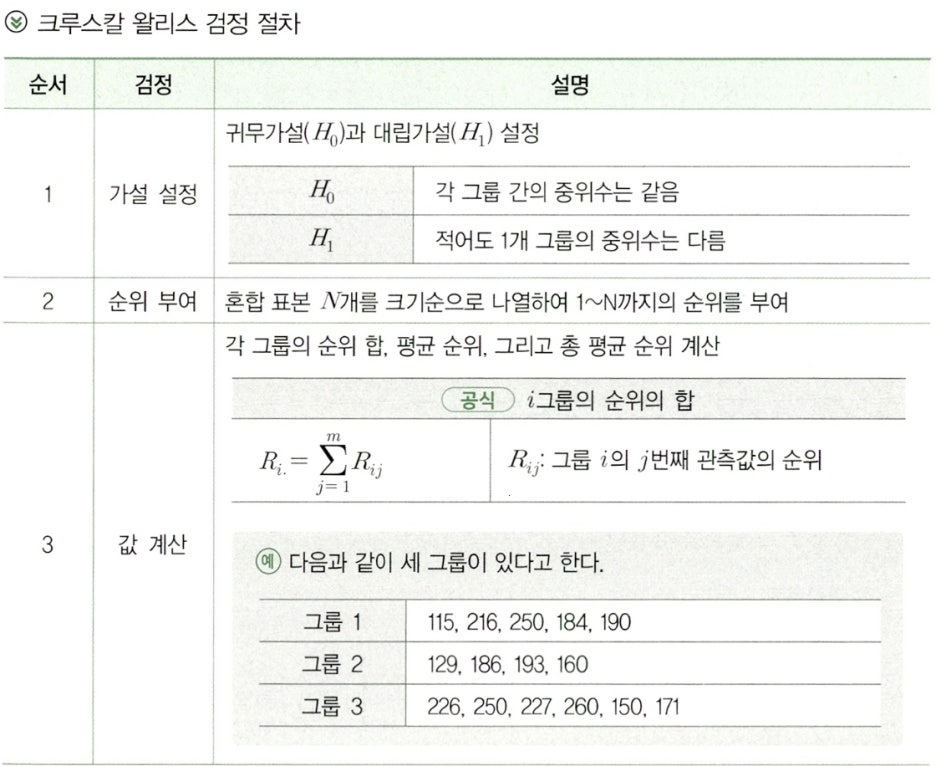
Clause 2. 크루스칼 왈리스 검정 절차

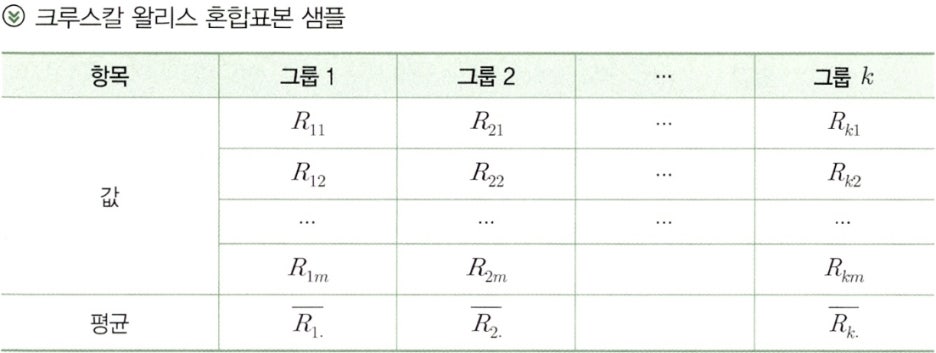
• 이해를 돕기 위하여 크루스칼 왈리스 혼합 표본 샘플 표를 참고하여 검정 절차를 설명한다.
• 각 그룹의 표본의 수는 아래 검정 절차의 예제와 같이 다를 수도 있다.

Subparagraph 6. 런 검정

Clause 1. 런 검정(Run Test) 개념

• 두 개의 값을 가지는 연속적인 측정값들이 어떤 패턴이나 경향이 없이 임의적으로 나타난 것인지를 검정하는 방법이다.
• 런(Run)은 동일한 측정값들이 시작하여 끝날 때까지의 덩어리를 말한다.

예)

동전의 앞면과 뒷면이 각각 1, 0이라고 할 때 ‘101001’이 나타났을 경우, 1/0/1/00/1로서 5개의 연속적인 런이라고 함

Clause 2. 런 검정 가정

• 이분화된 자료가 아닌 경우는 이분화된 자료로 변환시켜야 한다.
• 평균, 중위수, 최빈값 또는 사용자가 정의한 숫자 등의 기준값을 이용하여 이분화한다.

Clause 3. 런 검정 절차

런 검정 절차는 가설 설정, 검정 통계량, 기각역 검정으로 진행한다.