goaswon

Anyone.

2 minute read

Section 1. 데이터 탐색 기초

  • 데이터 탐색에서는 통계적인 방법을 통하여 데이터를 여러 각도에서 관찰하므로 기초통계량에 대한 이해가 중요하다.
  • 기초통계량을 중심 경향성, 산포도, 분포 측면으로 구분한다.

Paragraph 1. 중심 경향성의 통계량

데이터의 중심 경향성을 나타내는 통계량에는 평균, 중위수(또는 중앙값), 최빈값 등이 있다.

Subparagraph 1. 평균(Mean)

  • 평균은 변수의 값들의 합을 변수의 개수로 나눈 값이다.
  • 이상값에 의해 값의 변동이 심하게 변할 수 있다.

m = \frac{\text{sum of the terms}}{\text{number of terms}}

Subparagraph 2. 중위수(Median)

모든 데이터값을 크기 순서로 오름차순 정렬하였을 때 중앙에 위치한 데이터값으로, 중앙값이라고도 한다.

경우 중위수 구하는 방법
변수의 갯수가 홀수개 일 때 (n+1) / 2
변수의 갯수가 짝수개 일 때 n/2 번째와 (n+2)/2 번째 값의 평균

Subparagraph 3. 최빈값(Mode)

최빈값은 주어진 데이터 중에서 가장 많이 관측되는 수이다.

예) 주어진 데이터가 3, 5, 9, 4, 5 경우에 가장 많이 관측된 5가 최빈값

Paragraph 2. 산포도의 통계량

데이터의 흩어진 정도인 산포도를 표현하는 기초통계량에는 범위, 분산, 표준편차, 변동계수, 사분위 수 범위 등이 있다.

Subparagraph 1. 범위(Range)

  • 범위는 데이터값 중에서 최대 데이터값(Max)과 최소 데이터값(Min) 사이의 차이이다.

  • 범위(Range) = 최댓값 - 최솟값

    예) 주어진 값이 3, 5, 9, 4, 5 경우에 범위는 최댓값 (9) - 최솟값 (3) = 6

Subparagraph 2. 분산(Variance)

  • 데이터가 평균으로부터 흩어진 정도를 나타내는 기초통계량이다.
  • 편차(데이터 - 평균)의 합은 0이므로 편차의 제곱의 합을 이용하여 계산한다.
  • 모분산은 편차의 제곱의 합을 모집단의 수(N)로 나누어주고, 표본분산은 표본의 수에서 1을 뺀 자유도(n-1)로 나누어 계산한다.

⬇모분산

모분산

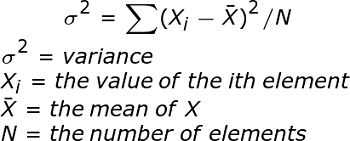
⬇표본분산

표본분산

S^2 = sample variance
x_i = the value of the one observation
\bar{x} = the mean value of all observations
n = the number of observations

Subparagraph 3. 표준편차(Standard Deviation)

  • 표준편차는 분산의 양(+)의 제곱근의 값이다.
  • 분산은 편차의 제곱을 했기 때문에 원래의 수학적 단위와 차이가 발생하므로 제곱근을 취한 값을 표준편차로 하고, 이 값을 통하여 평균에서 흩어진 정도를 나타낸다.

⬇모표준편차

\sigma={\sqrt {\frac {\sum(x_{i}-{\mu})^{2}}{N}}}

\sigma = population standard deviation
N = the size of the population
x_i = each value from the population
\mu = the population mean

⬇표본표준편차

\sigma={\sqrt {\frac {\sum(x_{i}-{\mu})^{2}}{N}}}

\sigma = population standard deviation
N = the size of the population
x_i = each value from the population
\mu = the population mean

Subparagraph 4. 변동계수(CV; Coefficient of Variation)

  • 측정 단위가 서로 다른 자료의 흩어진 정도를 상대적으로 비교할 때 사용한다.
  • 표준편차나 분산은 한 가지 자료의 산포도를 측정하는 데는 유용하지만 단위가 다른 두 자료 군의 산포도를 비교하는 데는 부적절하다.
  • 상대 표준편차라고도 한다.
  • 표준편차를 표본평균으로 나눈 값으로서 값이 클수록 상대적인 차이가 크다.
  • 평균과 표준편차를 나누어서 단위가 없으므로 서로 다른 단위의 산포도를 비교할 수 있다.

⬇변동계수

CV = \frac{\sigma}{\mu}

\sigma = population standard deviation
\mu = population mean

Subparagraph 5. 사분위 수 범위(IQR; InterQuartile Range)

  • 사분위 수 범위는 자료들의 중간 50%에 포함되는 자료의 산포도를 나타낸다.
  • 사분위 수 범위는 제1 사분위 수(Q_1)과 제3 사분위 수(Q_3) 사이의 차이이다.

⬇사분위 수 범위 구하는 방법

순서 방법 예시
1 자료들을 오름 차순으로 정렬 1, 5, 8, 9, 13, 17, 19
2 자료들의 중위수를 구함 7개의 자료로 홀수이므로 (7 + 1)/2 = 4번째 자료인 9가 중위수
3 중위수를 기준으로 좌측의 중위수(Q_1)와 우측의 중위수(Q_3)를 각각 구함 중위수를 기준으로 좌측(1 5 8)의 중위수(Q_1, 5)와 우측(1317 19)의 중위수(Q_3, 17)를 각각 구함
4 사분위 수 범위(IQR) = Q_3 - Q_1 에 대입하여 IQR을 구함 IQR = 17 - 5 = 12

Paragraph 3. 데이터의 분포를 나타내는 통계량

데이터의 분포가 좌/우로 치우친 정도에 따른 왜도(Skewness)와 정규 분포보다 뾰족한 정도를 나타내는 첨도(Kurtosis)로 데이터의 분포를 파악할 수 있다.

Subparagraph 1. 왜도(Skewness)

데이터의 분포가 정규 분포로부터 오른쪽 또는 왼쪽으로 치우친 정도를 보여주는 값이다.

⬇왜도 종류

종류 설명
왼쪽 편포(Skewed to the left) • 평균(Mean) < 중위수(Median) < 최빈값(Mode)
• 왼쪽 편포(왼쪽 꼬리 분포)의 왜도는 0보다 작음
오른쪽 편포(Skewed to the right) • 최빈값(Mode) < 중위수(Median) < 평균(Mean)
• 오른쪽 편포(오른쪽 꼬리 분포)의 왜도는 0보다 큼

왜도

Subparagraph 2. 첨도(Kurtosis)

  • 데이터의 분포가 정규 분포 곡선으로부터 위 또는 아래쪽으로 뾰족한 정도를 보여주는 값이다.
  • 정규 분포는 첨도가 3이지만 일반적으로 첨도의 정의에서 3을 뺀 0을 기준으로 하고 있다. 따라서 이 책에서도 정규 분포의 첨도를 0으로 한다.

왜도, 첨도의 구분

You May Also Enjoy